[DB] 함수 종속성

1. 함수 종속성

• 어떤 속성 A의 값을 알면 다른 속성 B의 값이 유일하게 정해지는 의존 관계를 다음과 같이 표현한다.
  • dependent: 속성 B는 속성 A에 종속한다
  • determine: 속성 A는 속성 B를 결정한다
  • 이것을 $A → B$ 로 표기하며, A를 B의 결정자라고 한다.

학생수강성적 릴레이션

학생번호	학생이름	주소	학과	학과사무실	강좌이름	강의실	성적
501	박지성	영국 맨체스타	컴퓨터과	공학관101	데이터베이스	공학관 110	3.5
401	김연아	대한민국 서울	체육학과	체육관101	데이터베이스	공학관 110	4.0
402	장미란	대한민국 강원도	체육학과	체육관101	스포츠경영학	체육관 103	3.5
502	추신수	미국 클리블랜드	컴퓨터과	공학관101	자료구조	공학관 111	4.0
501	박지성	영국 맨체스타	컴퓨터과	공학관101	자료구조	공학관 111	3.5

• 학생 번호를 알고있으면 학생 이름, 학과 등등을 결정할 수 있음
• 학과를 알고 있으면 학과 사무실 번호를 알 수 있음
  • 따라서 학생 번호를 알면 학과 사무실 번호를 알 수 있다.

---

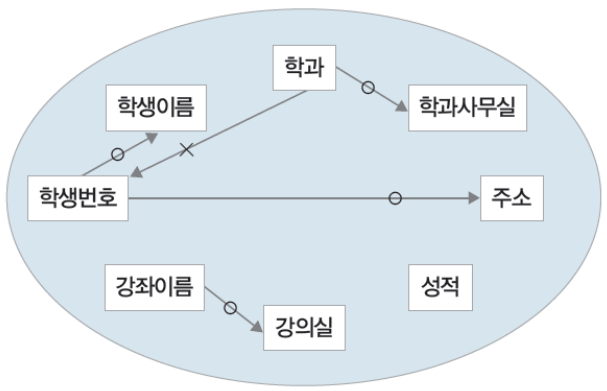
• 학생수강성적 릴레이션이 위와 같다고 할때, 각 속성 사이에는 의존성이 존재한다.

학생수강성적 릴레이에서의 예

• 종속관계에 있는 예
  • 학생번호 → 학생이름
  • 학생번호 → 주소
  • 강좌이름 → 강의실
  • 학과 → 학과사무실
• 종속하지 않는 예
  • 학생이름 → 강좌이름
  • 학과 → 학생번호
• 종속하는 것처럼 보이지만 주의 깊게 보면 그렇지 않은 예
  • 학생이름 → 학과

---

학생수강성적 릴레이션의 종속관계

• 아래 글 정리 필요 함수 종속성(FD, Functional Dependency) 릴레이션 R과 R에 속하는 속성의 집합 X, Y가 있을 때, X 각각의 값이 Y의 값 한 개와 대응이 될 때 ‘X는 Y를 함 수적으로 결정한다’라고 하고 X→Y로 표기함. 이때 X를 결정자(determinant)라고 하고, Y를 종속 속성 (dependent attribute)이라고 함. 함수 종속성은 보통 릴레이션 설계 때 속성의 의미로부터 정해짐.

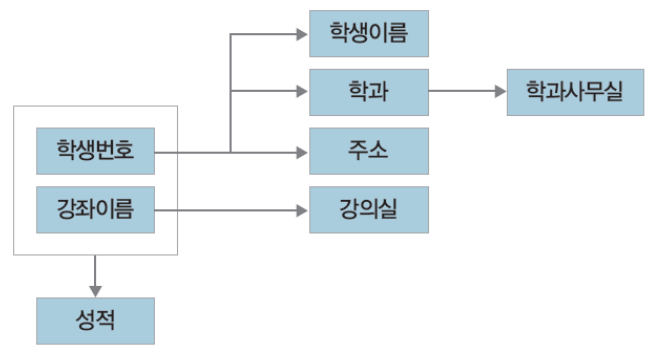
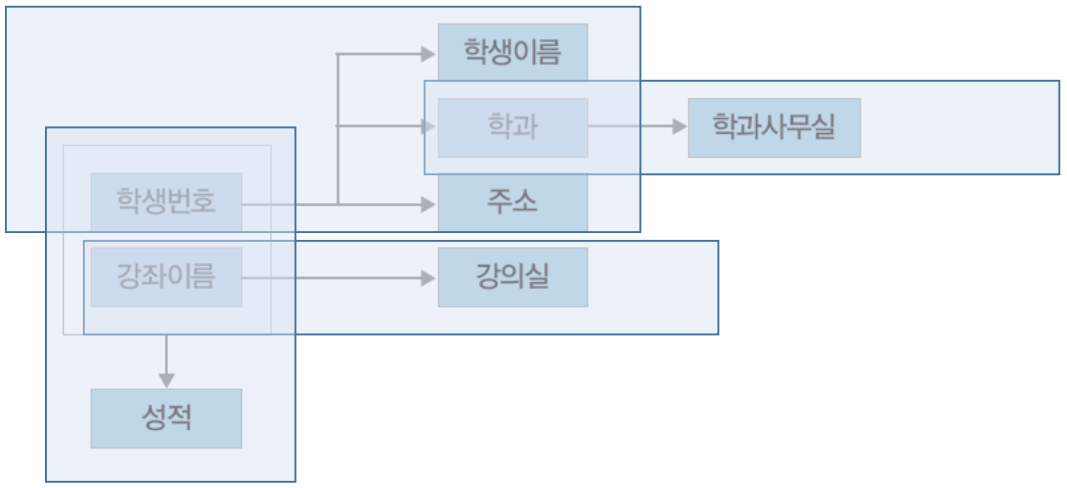
2. 함수 종속성 다이어그램

• 함수 종속성 다이어그램(functional dependency diagram): 함수 종속성을 나타내는 표기법
  • 릴레이션의 속성 : 직사각형
  • 속성 간의 함수 종속성 : 화살표
  • 복합 속성 : 직사각형으로 묶어서 그림

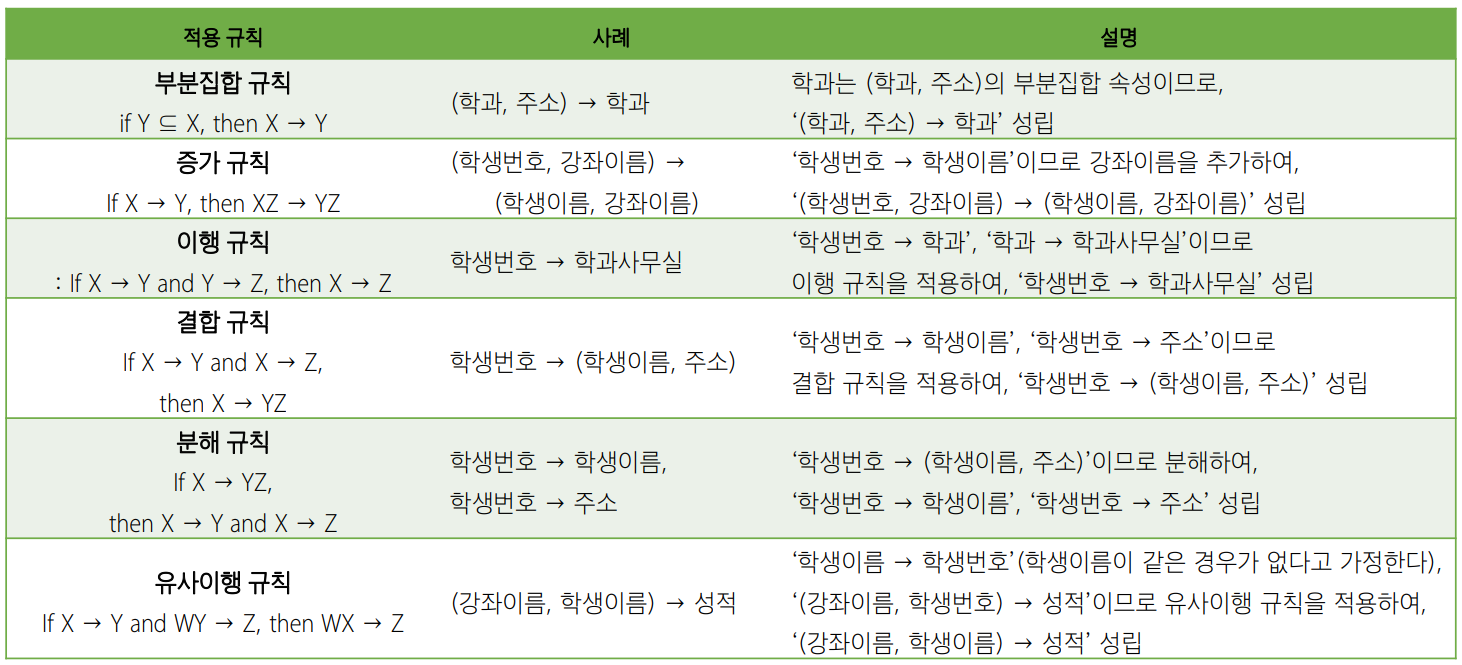
3. 함수 종속성 규칙

• $X, Y, Z$가 릴레이션 $R$에 포함된 속성의 집합이라 할 때, 함수 종속성에 관한 다음과 같은 규칙이 성립한다.

• 추후 수식 문법 등으로 재정리 필요

temp img: 추후 정리 필요

temp img: 추후 정리 필요

4. 함수 종속성과 기본키

• 릴레이션의 함수 종속성을 파악하기 위해서는 우선 기본키를 찾아야 함
• 기본키가 함수 종속성에서 어떤 역할을 하는지 알면 이상현상을 제거하는 정규화 과정을 쉽게 이해할 수 있음

temp img: 추후 정리 필요

• 예) 이름이 같은 학생이 없다고 가정하면, 이름 → 학과, 이름 → 주소, 이름 → 취득학점이므로 이름 → 이름, 학과, 주소, 취득학점이 성립한다. 즉 이름 속성이 학생 릴레이션의 전체를 결정함.

---

학생 릴레이션 예

이름	학과	주소	취득학점
박지성	컴퓨터과	영국 맨체스타	92
김연아	체육학과	대한민국 서울	95
장미란	체육학과	대한민국 강원도	98
추신수	컴퓨터과	미국 클리블랜드	99

---

5. 이상 현상과 결정자

• 이상현상은 한 개의 릴레이션에 두 개 이상의 정보가 포함되어 있을 때 나타남
  • 기본키가 아니면서 결정자인 속성이 있을 때 발생함
• 학생수강성적 릴레이션의 경우 학생 정보(학생번호, 학생이름, 주소, 학과)와 강좌 정보(강좌이름, 강의실)가 한 릴레이션에 포함되어서 이상현상이 나타남 (학과, 학생번호, 강좌이름은 기본키가 아니면서 결정자인 예이다)

학생수강성적 릴레이션의 함수 종속성 다이어그램

• 위 예시는 결정자가 너무 많아 기본키를 만들 수 없음

• 릴레이션이 너무 크다는 것임

• 학생수강성적 릴레이션을 분해하여 부분 릴레이션을 생성할 필요가 있음

• 5.1. 릴레이션의 분해

• 분해할 때 부분 릴레이션의 결정자는 원래 릴레이션에 남겨두어야 함
• 그래야 분해된 부분 릴레이션이 원래 릴레이션과 관계를 형성할 수 있음

릴레이션의 분해

1단계

• 학생수강성적 릴레이션에서 (강좌이름, 강의실)을 분리
  • 학생수강성적1(학생번호, 학생이름, 학과, 주소, 강좌이름, 성적, 학과사무실)
  • 강의실(강좌이름, 강의실)

2단계

• 학생수강성적1 릴레이션에서 (학생번호, 강좌이름, 성적)을 분리
  • 학생학과(학생번호, 학생이름, 학과, 주소, 학과사무실)
  • 학생성적(학생번호, 강좌이름, 성적)
  • 강의실(강좌이름, 강의실)

3단계

• 학생학과 릴레이션에서 (학과, 학과사무실)을 분리
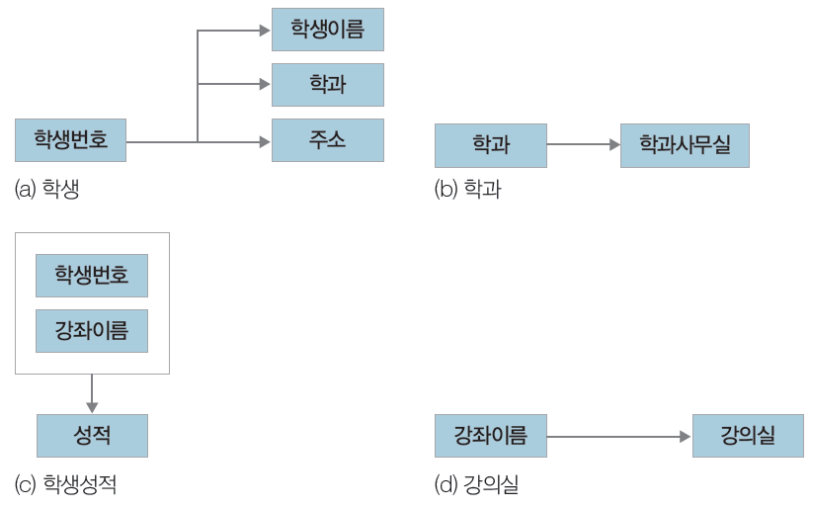
  • 학생(학생번호, 학생이름, 학과, 주소)
  • 학과(학과, 학과사무실)
  • 학생성적(학생번호, 강좌이름, 성적)
  • 강의실(강좌이름, 강의실)

---

분해 결과

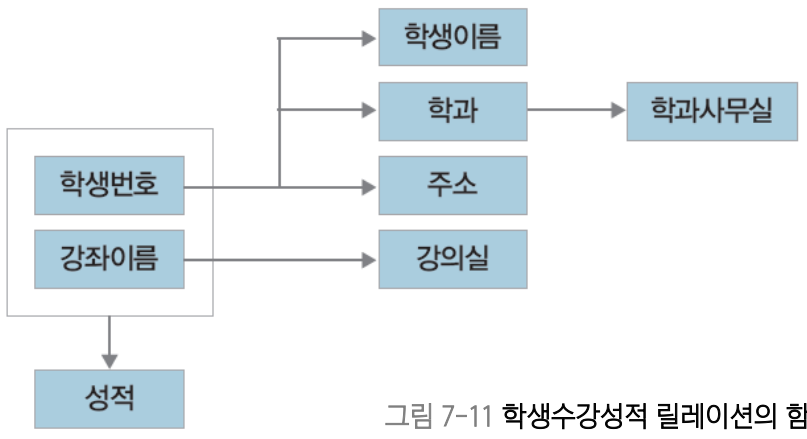
학생수강성적 릴레이션을 분해한 결과

---

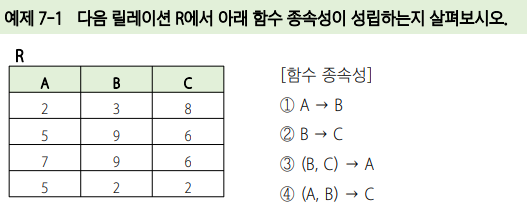
함수 종속성 예제

• 시험에서 비슷한 문제 내니까 반드시 공부!!

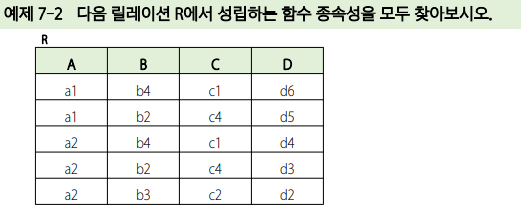
• 함수 종속성은 보통 릴레이션을 설계할 때 속성의 의미로부터 정해지지만, 역으로 릴레이션에 저장된 속성값으로부터 추정할 수 있음.

temp img: 추후 정리 필요

temp img: 추후 정리 필요

결정자가 한개인 것을 먼저 찾아야 함, 그리고 결정자가 두개, 세개, 그 이상인 경우를 모두 찾아야한다.

찾을 때 종속성 규칙을 사용해 더 쉽게 찾을 수 있음

• 풀이

• 결정자가 한 개인 경우 : B → C, C → B, D → A, D → B, D → C
• 결정자가 두 개인 경우 : AB → C (B → C 이므로 AB → C 는 함수종속성 규칙에서 당연히 성립한다.) AB → D AC → B (함수종속성 규칙에서 당연히 성립) AC → D AD → B (함수종속성 규칙에서 당연히 성립) …
• 결정자가 세 개인 경우 : ABC → D (함수종속성 규칙에서 당연히 성립) … 등
• 정답은 당연히 성립하는 것들을 제외한 다음 규칙만 적어주면 된다. B → C, C → B, D → A, D → B, D → C, AB → D, AC → D

---