[OS] 페이징 개요

게시 2024/05/29 업데이트 2024/09/04

By Jangan Lee 읽는 시간 43분

1. 가상 메모리 사용 이유

프로그램을 실행하려면 정확한 주소가 필요하다. 메모리 주소가 1이라도 다르면 프로그램은 정상적으로 실행되지 않는다. 그런데 만약 개발자가 시스템 메모리 크기까지 고려하면서 프로그래밍을 개발해야 한다고 하자. 그러면 다음과 같은 문제점 및 제한점이 존재한다.

다중 프로그램시 주소 충돌 가능성 있음
특정 시스템에 종속적인 프로그램밖에 만들 수 없음
- 프로그램이 어디 위치에 설치되는 지 모름

이런 문제를 해결하기 위해 메모리는 무조건 0번지부터 다 쓴다고 가정하였으며, 주소 변환을 위해 MMU를 사용하였다.

1.1. 연속 메모리, segmentation 단점

프로그램이 1~2개일 땐 문제 없으나 여러개일 수록 관리 어려움
Segment 크기가 클 수록 메모리 할당이 더 어려워짐
- External fragmentation 문제: 잦은 defragmentation 동반됨
관리가 더 어려워짐
- 크기가 제각각인 책을 책장에 가지런히 보이게 꽂는 것과 비슷함
  - 하지만 책의 크기가 균일하면 어떨까?: 상대적으로 관리하기 쉬움
- 관리 어려움 → 검색 효율 저하 → 메모리 운용 속도 저하

2. 페이징

고정-분할 방식을 이용한 가상 메모리 관리 기법

2.1. 용어

2.1.1. 페이지(Page)

코드, 데이터, 스택 등 프로세스의 구성 요소에 상관없이 고정 크기로 분할한 단위
프로세스의 주소 공간을 0번지부터 동일한 크기의 페이지(page)로 나눔
페이지의 크기
- 주로 4KB. 운영체제마다 다르게 설정 가능, 2n. 즉 4KB, 8KB, 16KB 등
프로세스 하나를 책 한권이라고 보자.
프로세스 내 메모리 내용 하나하나를 페이지라고 보자.

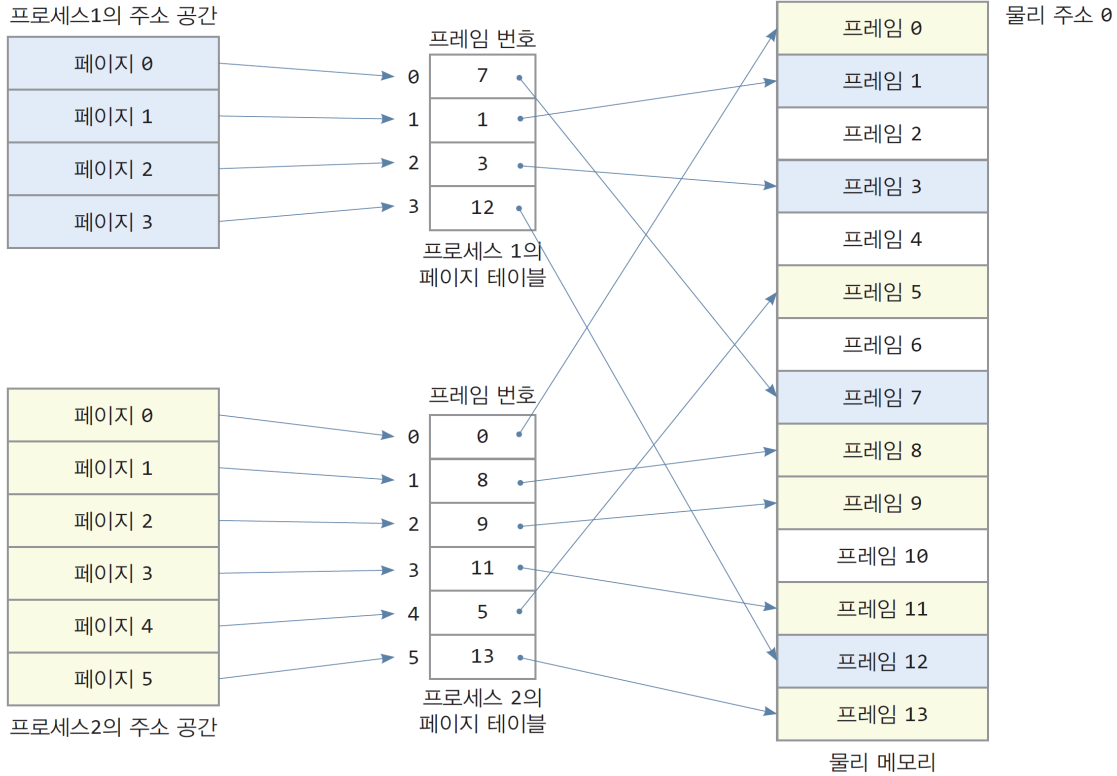
2.1.2. 페이지 프레임(Page frame)

물리 메모리 역시 0번지부터 페이지 크기로 나누고, 프레임(frame)이라고 부름
페이지와 프레임에 0번부터 순서대로 번호 붙임
페이지 크기 == 페이지 프레임 크기

2.1.3. 페이지 테이블

각 페이지에 대해 페이지 번호와 프레임 번호를 1:1로 저장하는 테이블

2.2. 논리페이지와 물리 프레임 매핑

메모리 두번 접근하기 때문에 속도가 느리다! 해결방법은?

2.3. 페이징을 사용하는 이유

용이한 구현
- 메모리를 0번지부터 고정 크기로 단순히 분할하기 때문
높은 이식성
- 페이징 메모리 관리를 위해 CPU에 의존하는 것 없음
- 다영한 컴퓨터 시스템에 쉽게 이식 가능
높은 융통성
- 시스템에 따라 응용에 따라 페이지 크기 달리 설정 가능
메모리 활용과 시간 오버헤드면에서 우수
- 외부 단편화 없음
- 내부 단편화는 발생하지만 매우 작음
- 홀 선택 알고리즘을 실행할 필요없음

2.4. 페이징과 단편화

외부 단편화는 발생하지 않음
- 불필요한 defragmentation과정이 필요 없음
내부 단편화는 발생
- 페이지 한칸을 할당 받았는데 그곳들 다 못채운다면 내부 단편화
페이지 구조에서 최대 내부 단편화 크기(worst case):
- $($ 단일 페이지크기 $-1) \times$ 페이지 갯수
  - 모든 페이지에 1바이트씩만 점유하고 있는 상태
  - 하지만 이럴 일은 없다!
  - 내부 단편화의 크기를 줄이는법: 프레임 크기를 줄이면 됨
일반적으로 프로세스의 마지막 페이지에서만 단편화가 발생함
- (스택-힙은 가변이니깐 제외한다 치고)
- 보통 페이지 크기의 1/2 정도로 본다.
외부단편화 해결에 드는 비용에 비하면 매우 적은 비용이다.

2.5. 페이징 정리

32비트 CPU에서 페이지 크기가 4KB인 경우를 가정하자.

페이지 이용 시 물리 메모리의 최대 크기는?
- 페이지는 그저 메모리 운용을 어떻게 할 것인지에 관한 정책에 관한 것
- 물리 메모리 크기와는 상관 X: 최대 물리주소의 범위는 0~2^32-1=4GB
프로세스 주소 공간의 크기
- 마찬가지로 페이징은 메모리 운용과 관련된 정책으로 크기와는 무관함
- 가상 메모리 크기 == 물리메모리 최대 크기로 4GB
프로세스당 최대 페이지 개수
- 프로세스 메모리 공간을 4KB로 나누면 됨
- 4GB / 4KB = 2^20 = 약 100만 개
페이지 테이블 크기
- 페이지 테이블 항목(entry) 크기가 32비트라고 가정(페이지 번호 저장하기 위해)
- 그러면 4바이트 * (최대 페이지 수) = 4*2^20 = 4MB

3. 페이징 예제

4GB 메모리 공간, 페이지 크기는 4KB로 가정한다.

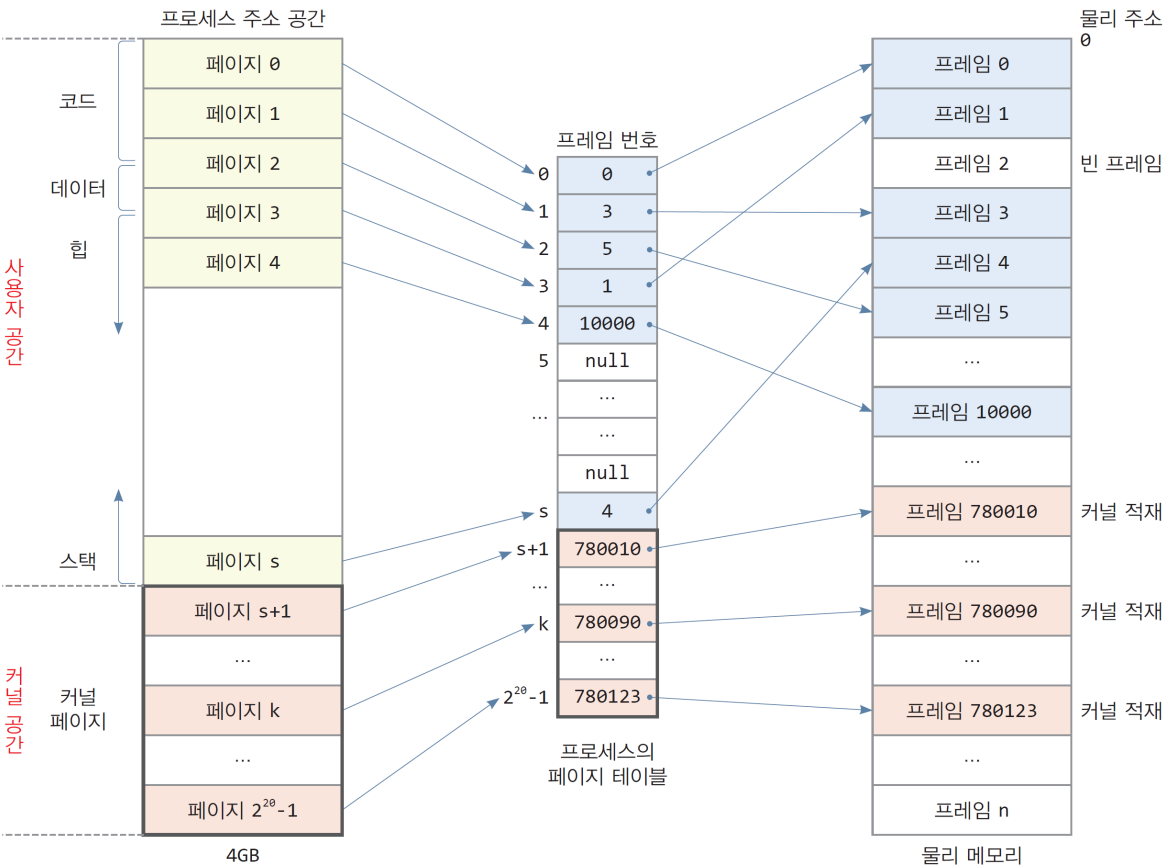
3.1. 프로세스

코드
- 페이지 0 ~ 페이지 2에 걸쳐 있음
데이터
- 페이지 2 ~ 페이지3에 걸쳐 있음
힙
- 페이지 3 ~ 페이지 4에 걸쳐 있음
스택
- 사용자 공간의 맨 마지막 페이지에 할당, 1페이지 사용
총 6개의 페이지, 점유중인 물리메모리 크기: 6 x 4KB = 24KB

4GB / 4KB = 1,000,000개: 페이지 엔트리 개수

3.2. 페이지 테이블

페이지 테이블은 주소 공간의 모든 페이지를 나타낼 수 있는 항목을 포함
현재 6개의 항목만 사용. 대부분의 항목은 비어 있음

동적할당 예

만약에 프로세스가 새로운 공간을 동적 할당을 받고, 데이터를 저장 하고, 해제를 한다면?

  
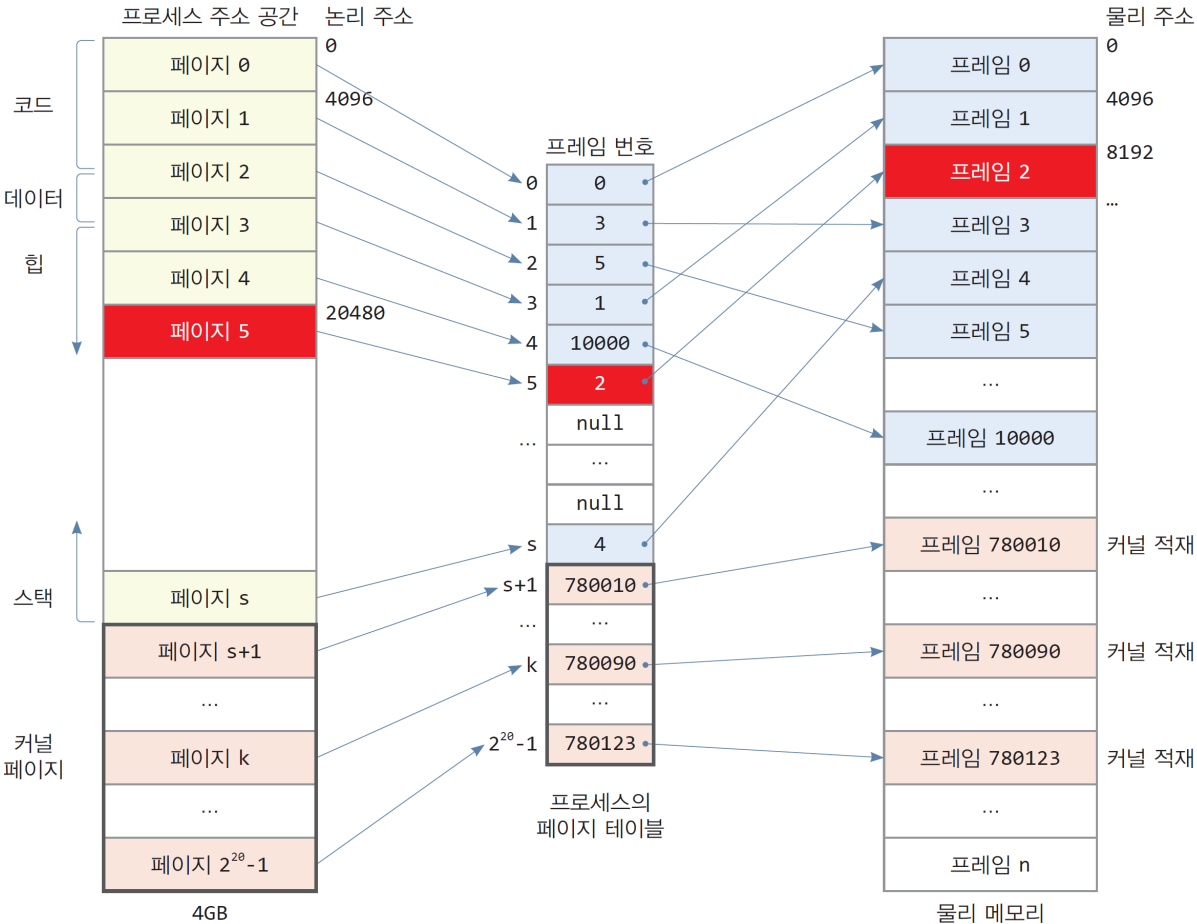
char *p = (char*) malloc(200); // 200 bytes on the heap
*p = "hello"; // 20480에 "hello"를 저장
free(p); // 20480 번지 해제

char *p = (char*) malloc(200);
- 1 페이지(4KB) 할당: 논리 페이지 5 할당, 물리 프레임 2 할당
- 페이지 5의 논리 주소 : 5 $\times$ 4KB = 20KB = 20 $\times$ 1024 = 20480 번지
- 프레임 2의 물리 주소 : 2 $\times$ 4KB = 8192 번지 - malloc(200)은 페이지 번호 5의 논리 주소 20480을 리턴
*p = "hello";
- 논리주소 20480이 MMU에 의해 물리주소 8192로 바뀜
- 물리주소 8192~8197번지에 h,e,l,l,o,\0 저장
free(p);
- 반환 후 페이지 5 전체가 비게 되므로, 페이지 5와 프레임 2가 모두 반환됨

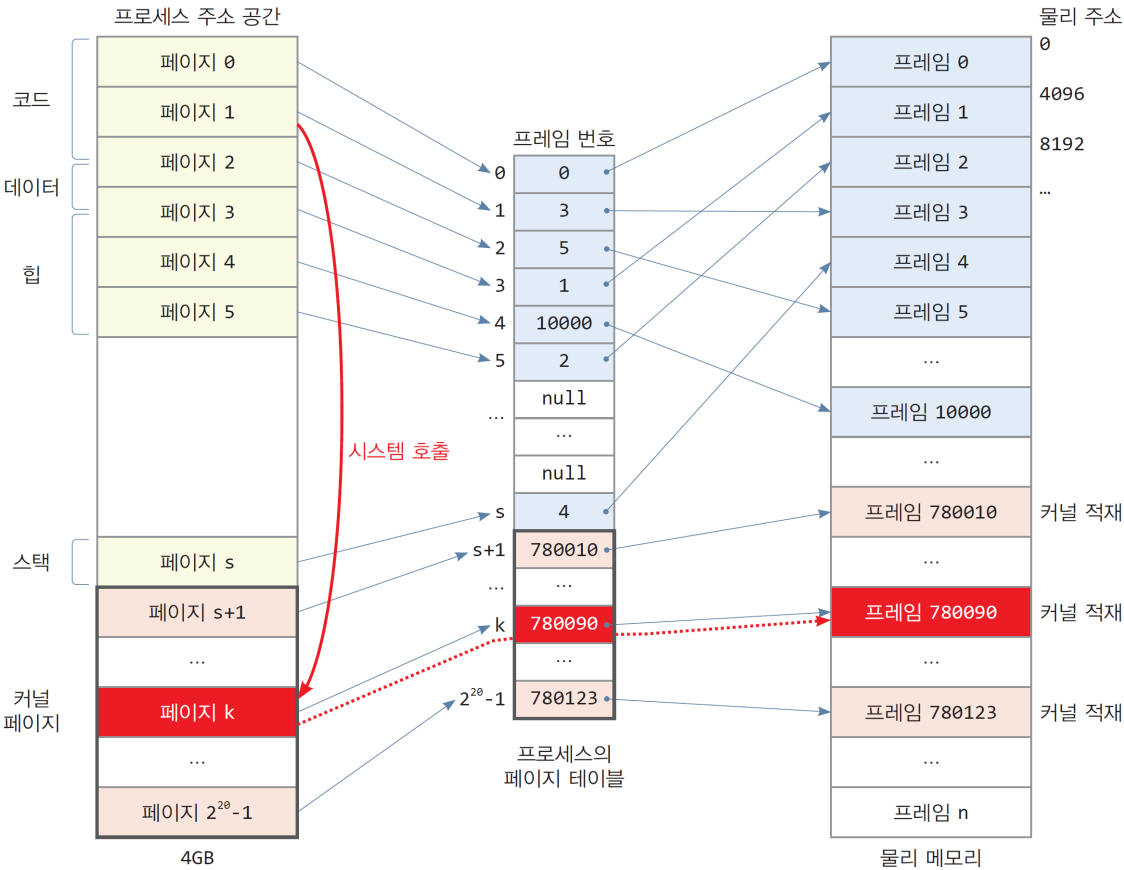
시스템 호출 예

System call을 호출한다면?
커널 코드도 논리 주소로 되어 있음
- 시스템 호출을 통해 커널 코드가 실행될 때 현재 프로세스의 페이지 테이블을 이용하여 물리 주소로 변환됨
  - 커널 공간의 페이지 k에 담긴 커널 코드 실행
  - 현재 프로세스 테이블에서 페이지 k의 물리 프레임 780090을 알아내고 해당 프레임에 적재된 커널 코드 실행

4. 페이징 구현

하드웨어 지원
- CPU의 지원
- CPU에 페이지 테이블이 있는 메모리 주소를 가진 레지스터 필요
- Page Table Base Register(PTBR) - MMU 장치
- 논리 주소의 물리 주소 변환 - 페이지 테이블 참조
- 페이지 테이블을 저장하고 검색하는 빠른 캐시 포함
- 메모리 보호 - 페이지 번호가 페이지 테이블에 있는지, 옵셋이 페이지의 범위를 넘어가는지 확인
운영체제 지원
- 프레임의 동적 할당/반환 및 페이지 테이블 관리 기능 구현
- 프로세스의 생성/소멸에 따라 동적으로 프레임 할당/반환
- 물리 메모리에 할당된 페이지 테이블과 빈 프레임 리스트 생성 관리 유지
- 컨텍스트 스위칭 때 CPU의 레지스터에 적절한 값 로딩

5. 페이징 주소 관리

5.1. 주소 변환

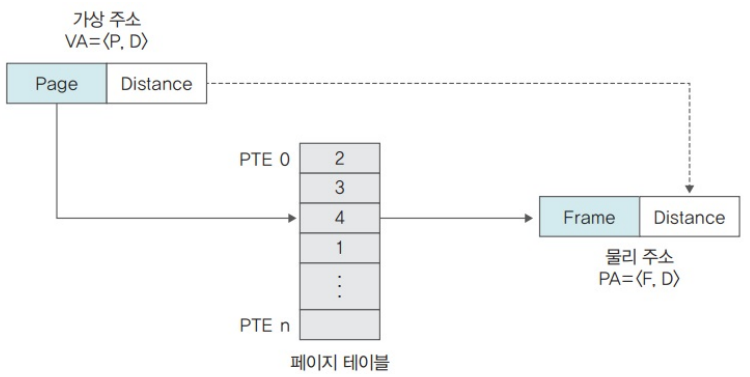
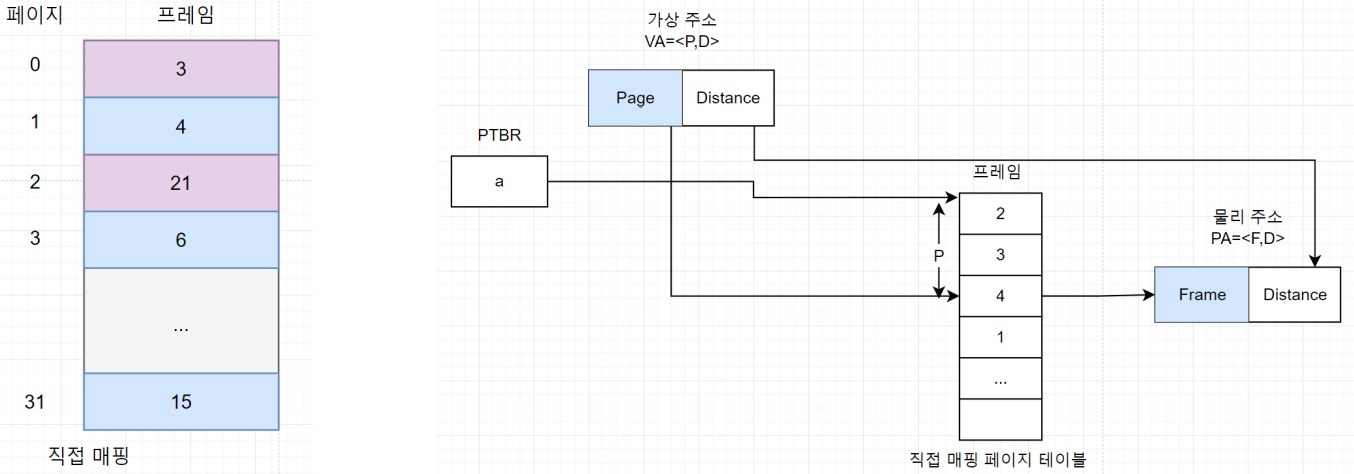
페이징에서는 가상 주소를 VA = <P, O>로 표현한다.

VA: 가상 주소(Virtual address)
P: 페이지 번호(Frame number)
O: 페이지의 처음 위치에서 해당 주소까지의 거리(Offset, distance)

물리 주소를 PA = <F, O>로 표현한다.

PA: 물리 주소(Physical address)
F: 프레임 번호(Frame number)
O: 프레임의 처음 위치에서 해당 주소까지의 거리(Offset, distance)
예: 페이지 크기가 10B일 때 가상주소 32번지? : VA = <3, 2>
예: 페이지 크기가 512B일 때 가상주소 2049번지? : <4, 1>

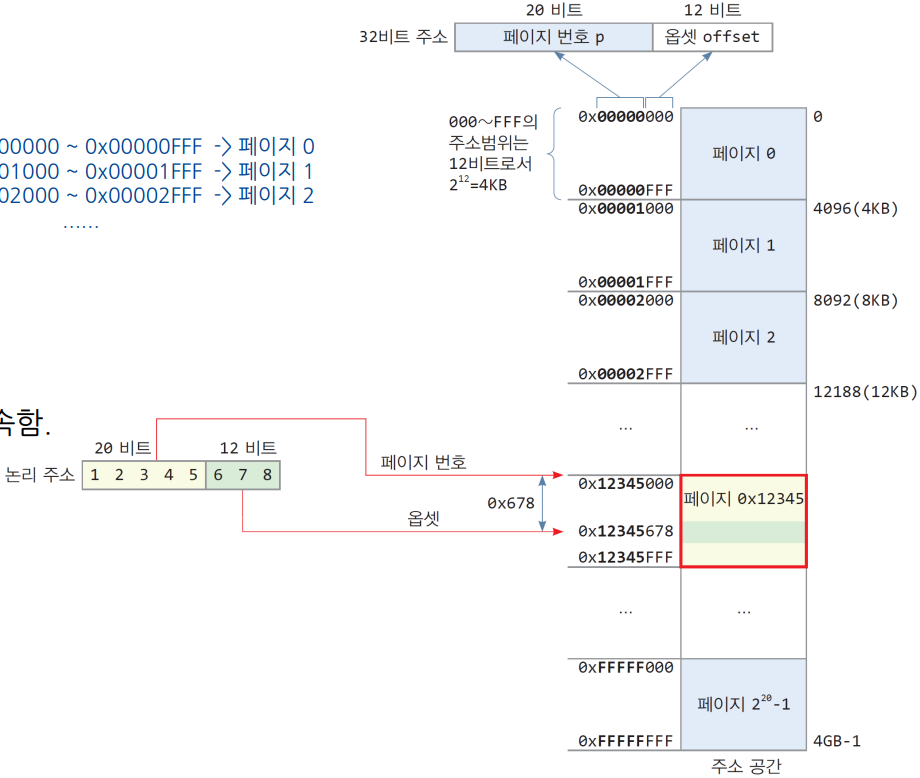
5.2. 페이징의 논리 주소 구성

[페이지 번호(p), 오프셋(offset)] ⇒ virtual address (VA)
- 페이지 크기가 4KB(=2^12)라면, 페이지 내를 표현하기 위해 필요한 주소공간은 12비트 크기.
- 즉, 오프셋은 12비트로 표현이 됨.
32비트 논리 주소 체계에서,
- 상위 20비트는 페이지 번호
- 하위 12비트는 옵셋
- 예, 가상주소 0x12345678의 경우,
- 0x12345678는 0x12345000 ~ 0x12345FFF에 속함. 페이지 12345. 따라서, VA = <12345, 678>

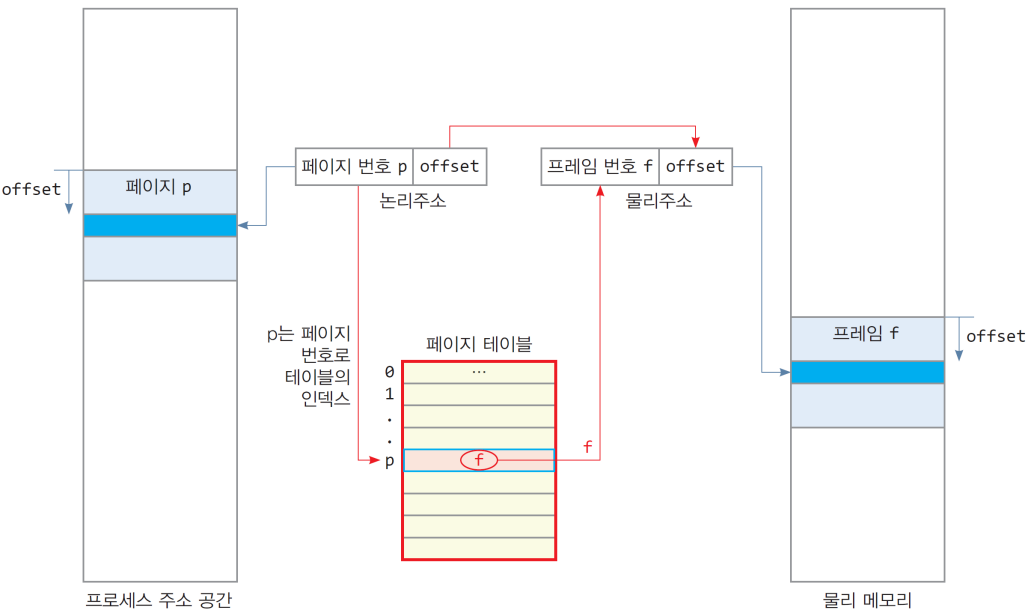
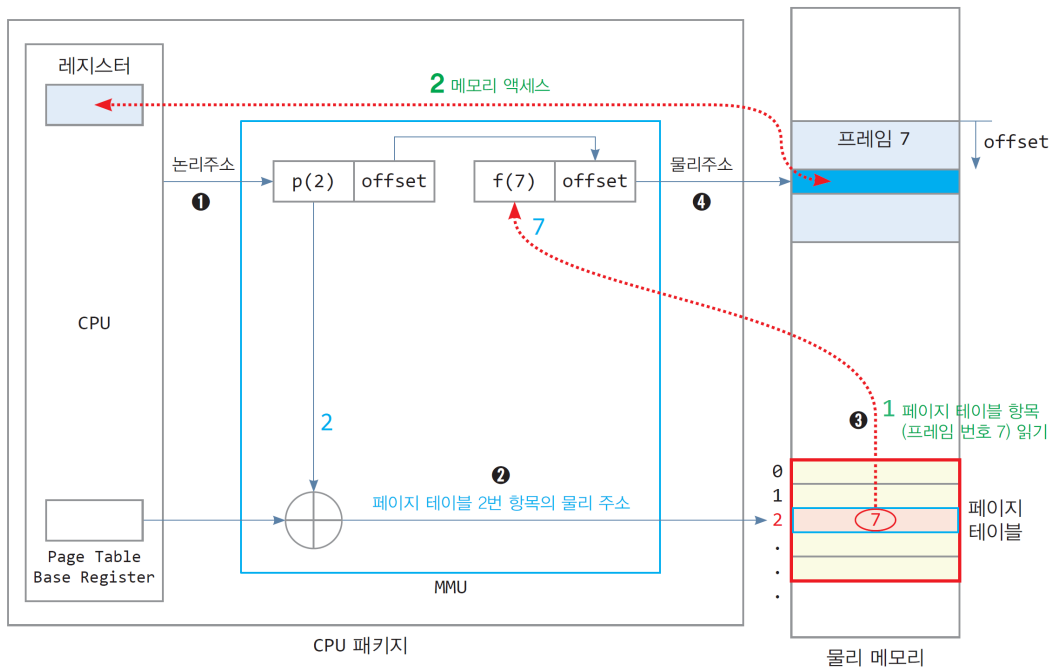
5.3. 페이지 주소의 물리주소 변환

이후 페이지 테이블에서 물리 페이지 주소 (i.e., frame)을 확인하여 주소를 확인후, 해당 프레임에 접근하고 678만큼 떨어진 위치에 접근.

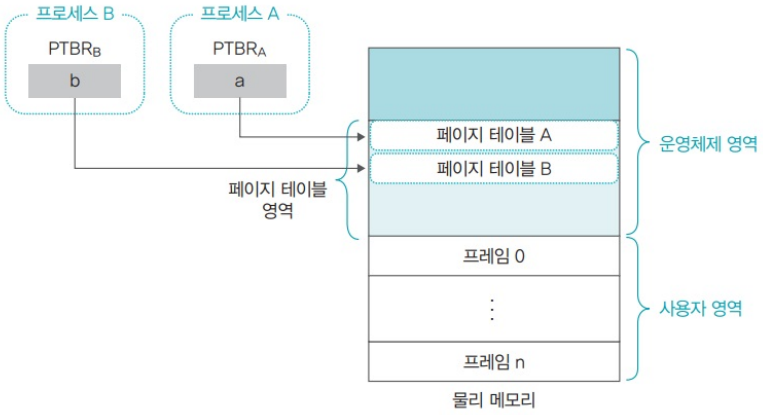
5.4. Page table base Register

페이지 테이블 기준 레지스터(PTBR): 프로세스가 페이지 테이블에 빠르게 접근하기 위한 레지스터
- 각 페이지의 테이블 시작 수조는 PTBR에 저장됨
- Context switching시에는 PCB에 저장

6. 페이지 테이블 매핑

페이지 테이블도 메모리에 있는 자료구조! 즉, Swap의 대상이 됨.
테이블 자체의 관리 방식에 따라 ‘가상주소→물리주소’ 변환방법이 달라짐
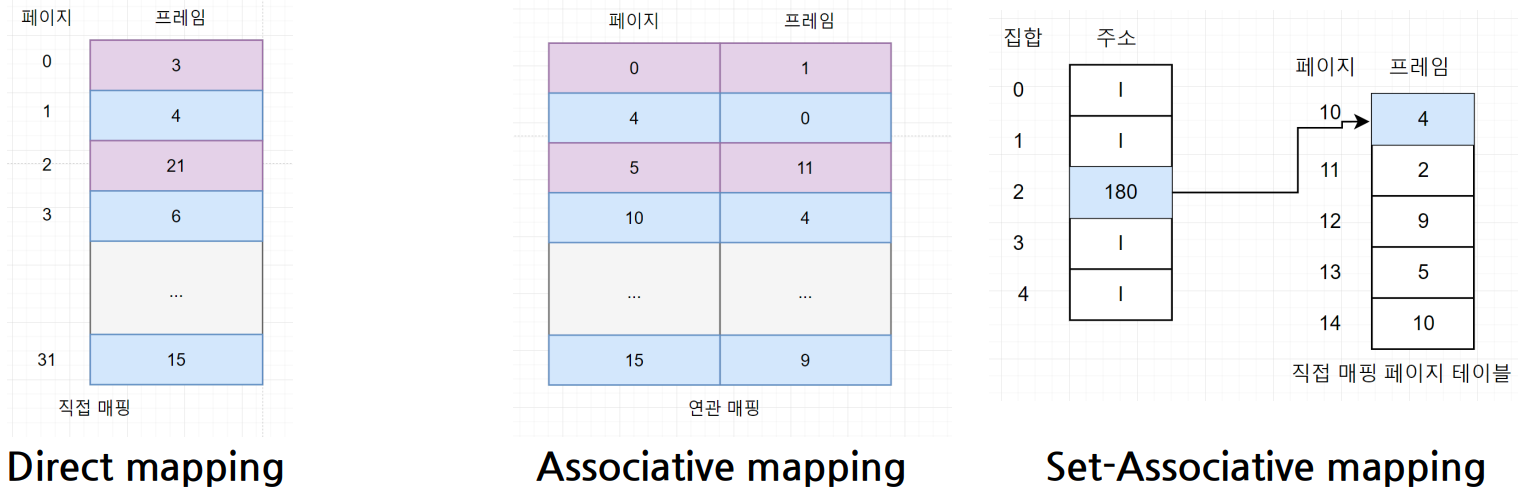
- 직접매핑: 메모리 주소와 페이지의 순서를 일치시켜 매핑(e.g., 동일한 배열을 가지도록)
- 연관매핑: 일부 페이지만 저장. 순서도 무작위. 전체 테이블에 대한 검색 필요
- 집합-연관매핑: 둘의 하이브리드. 순서를 일치시키되, 일정 그룹을 두어 그룹내에서 저장.

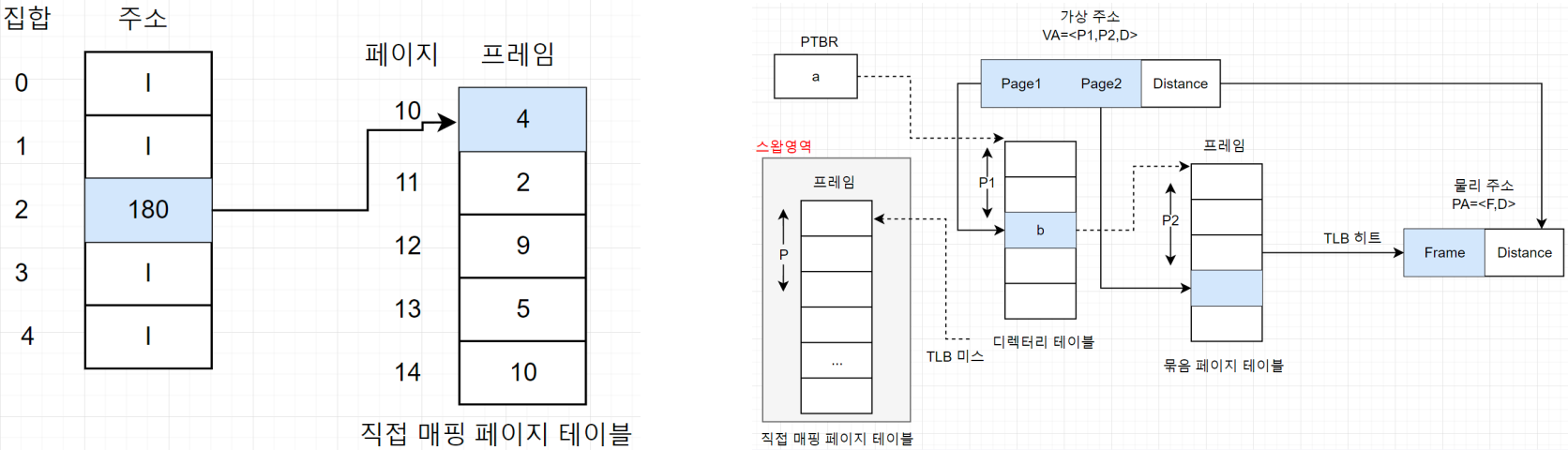
6.1. 직접 매핑

페이지 테이블 전체가 물리 메모리의 운영체제 영역에 존재.
- 모든 페이지 테이블을 물리 메모리에 가지고 있는 가장 단순한 방식
- 별다른 부가 작업 없이 바로 주소 변환이 가능하기 때문에 직접 매핑이라 부름.
모든 페이지를 물리 메모리에 가지고 있기 때문에 주소 *변환 속도가 빠름
- 단 용량낭비가 심함.

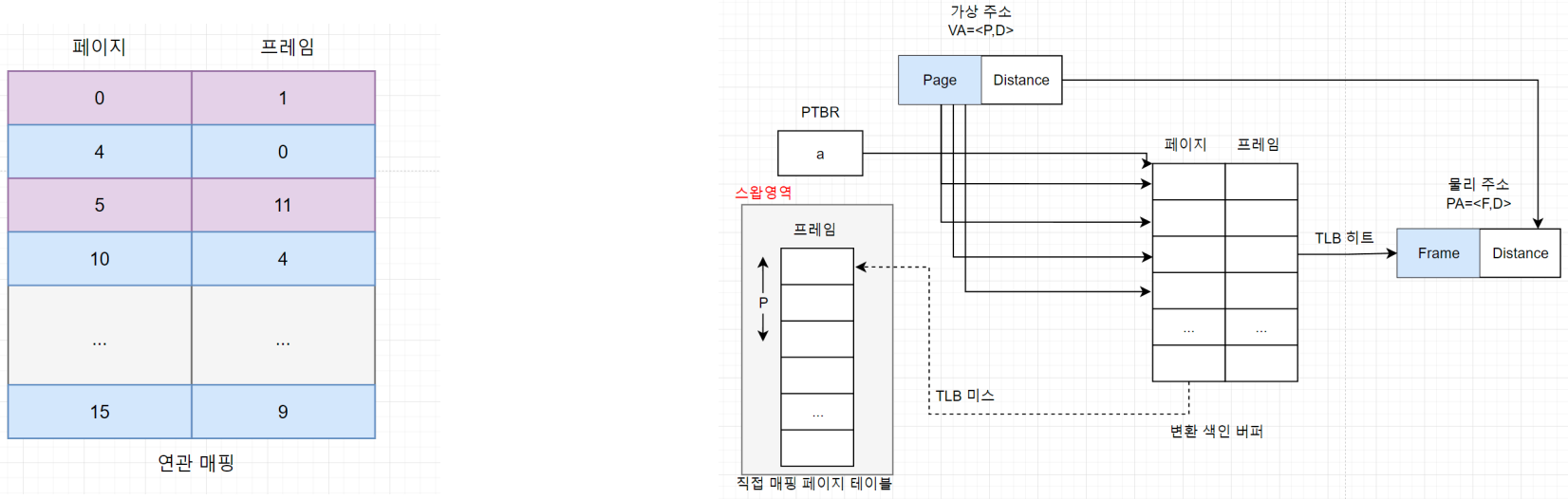
6.2. 연관 매핑

일부 페이지 정보만 물리메모리 상 테이블에서 관리.
- 보통 실제 물리 메모리에 올라와있는 페이지만 관리! → 용량 절약
- 나머지는 스왑 영역에… → 스왑영역에 따로 전체 테이블(i.e., 직접매핑)이 있음
- 연관매핑 테이블은 저장된 페이지와 프레임번호가 함께 저장함.
저장된 페이지 번호에는 순서가 따로 없음. → 페이지 참조시 모든 테이블 검색 필요.
- 병렬로 처리하기 위한 별도의 로직을 가지고 (복잡!), TLB / 연관레지스터 등으로 캐시
- 미스나면 스왑영역에 대한 검색이 다시 필요. 느림!

6.3. 집합-연관 매핑

집합-연관 매핑은 연관 매핑의 문제를 개선한 방식
- 연관 매핑 문제점: 만약 메모리에 없으면? 스왑영역의 모든 테이블을 검색해야함
페이지 테이블을 같은 크기의 여러 묶음으로 나누고, 그 묶음의 시작 주소를 가진 Set table(or directory table)을 만들어 관리함.
- 페이지 테이블 참조시, 디렉토리 테이블을 먼저 참조하여 물리메모리 상에 있는지 확인하고, 있다면 해당 주소를 참조하여 필요한 프레임 번호 매핑.
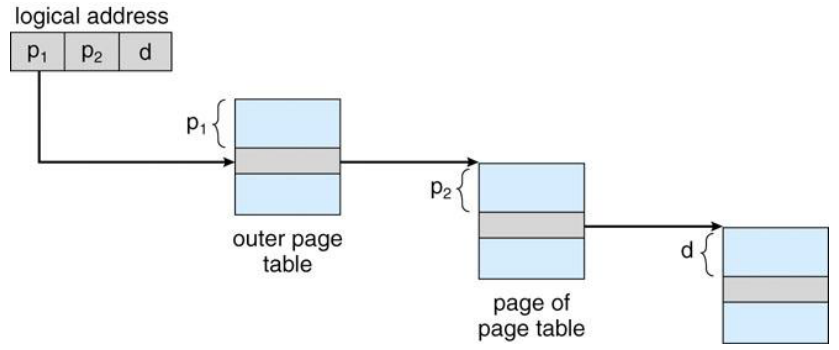
- VA = <P1, P2, O>

7. 페이지 테이블 관리

7.1. 관리가 쉽지 않은 이유

시스템에 여러 개의 프로세스가 존재하고, 프로세스마다 페이지 테이블이 하나씩 있음
메모리 관리자는 특정 프로세스가 실행될 때 마다 해당 페이지 테이블을 참조하여 가상 주소를 물리 주소로 변환하는 작업을 반복
- 페이지 테이블은 메모리 관리자가 자주 사용하는 자료 구조이므로 필요시 빨리 접근되어야 함
- 따라서 페이지 테이블은 물리 메모리 영역 중 운영체제 영역(커널)의 일부에 모아둠.
- 페이지 테이블의 수가 늘어나거나 페이지 테이블의 크기가 늘어나면 운영체제 영역이 그만큼 늘어나 사용자 영역이 줄어듬

7.2. 문제점

1번에 메모리 액세스를 위한 2번의 물리 메모리 액세스가 필요
- 페이지 테이블은 몇 MB의 크기로 메모리에 저장
- CPU가 메모리를 액세스할 때 마다, 2번의 물리 메모리 액세스 -> 실행 속도 저하시킴
- (페이지 테이블을 읽기 위해 1회, 진짜 데이터를 참조하기 위해 1회, 총 2회)
페이지 테이블의 낭비
- 대다수의 프로세스가 모든 메모리 공간을 다 쓰진 않는다… → 실제크기는 작음
- 따라서 대부분의 페이지 테이블 항목이 비어 있게됨…
  - 페이지 테이블은 프로세스의 최대 크기를 기준으로 형성
페이지 테이블도 스왑 대상! (We did it!)
- 물리 메모리의 크기가 작을 때는 프로세스만 스왑 영역으로 옮겨지는 것이 아니라 페이지 테이블의 일부도 스왑 영역으로 옮겨짐

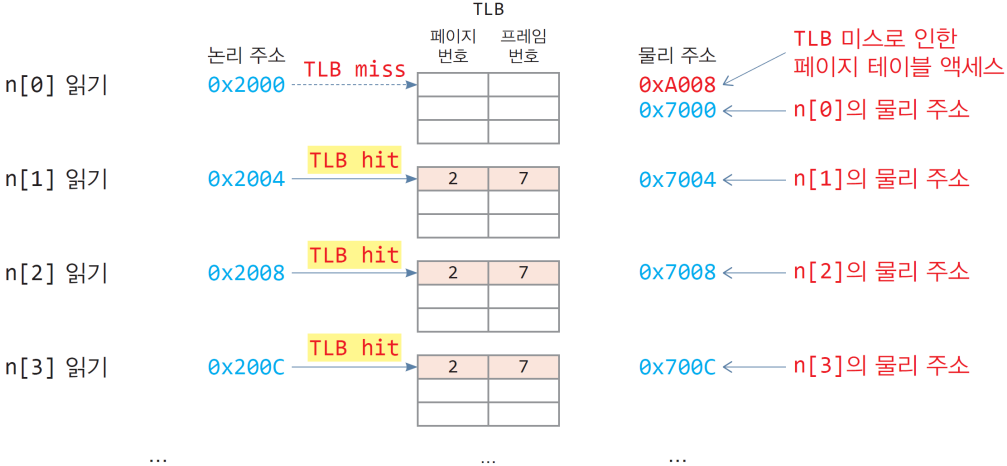
7.2.1. 메모리 2회 접근 문제

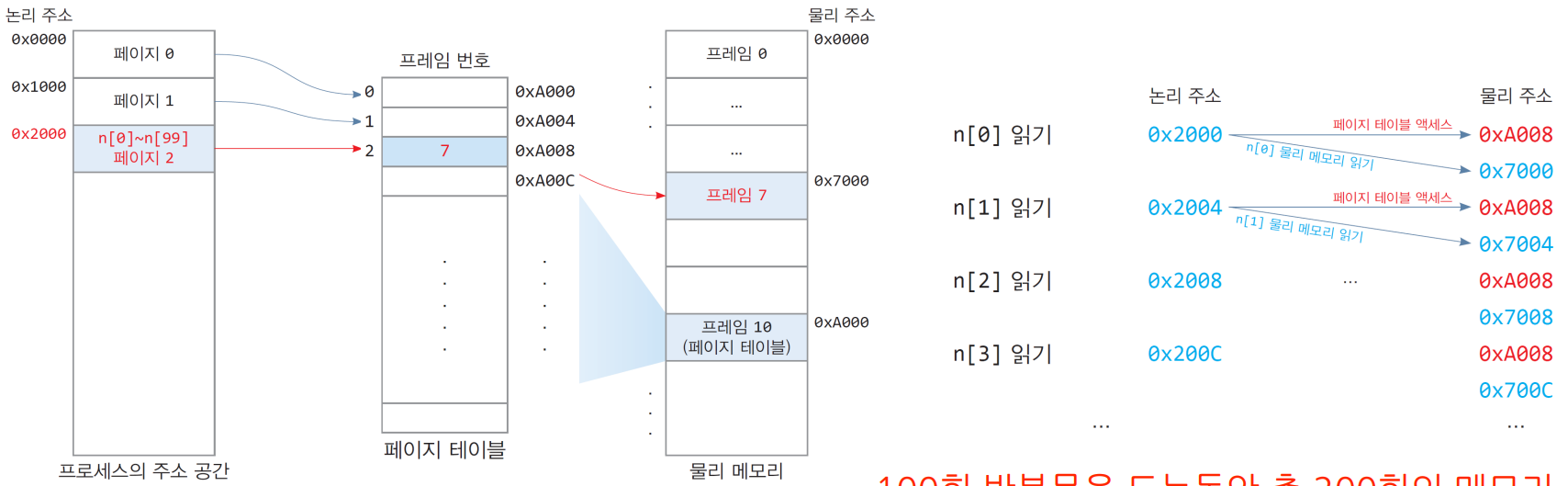
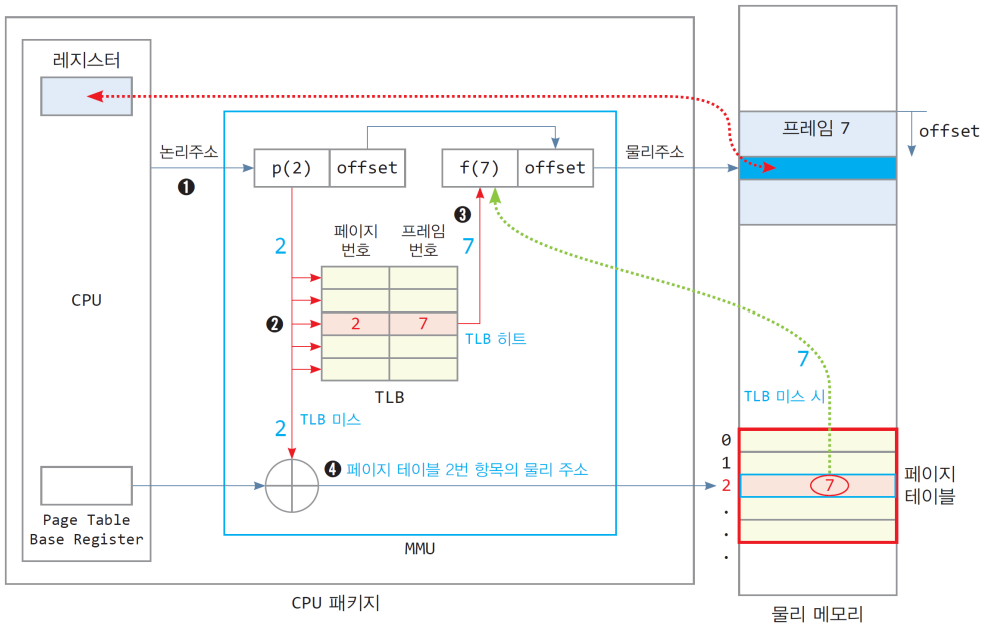
가정
- 32비트 CPU, 페이지는 4KB
- 배열 n[100]의 논리 주소는 0x2000(페이지 2)부터 시작
- 배열 n[100]의 물리 주소는 0x7000(프레임 7)부터 시작
- 배열 n[100]의 크기는 400바이트이며 페이지2에 모두 들어 있음
- 페이지 테이블 2번의 주소: 0xA008
- 페이지 테이블은 물리 메모리 0xA000번지부터 시작

코드

  
int n[100]; // 400바이트
int sum = 0;
for(int i=0; i<100; i++)
    sum += n[i];

100회 반복문을 도는 동안 총 200회의 메모리에 접근한다!

해결: TLB

변환 색인 버퍼(TLB, Translation Look-aside Buffer)
- 논리 주소를 물리 주소로 바꾸는 과정에서 페이지 테이블을 읽어오는 시간을 없애거나 줄이는 기법 → 페이지 접근에 대한 캐시를 두자!
TLB(Translation Look-aside Buffer) a.k.a., address translation cache
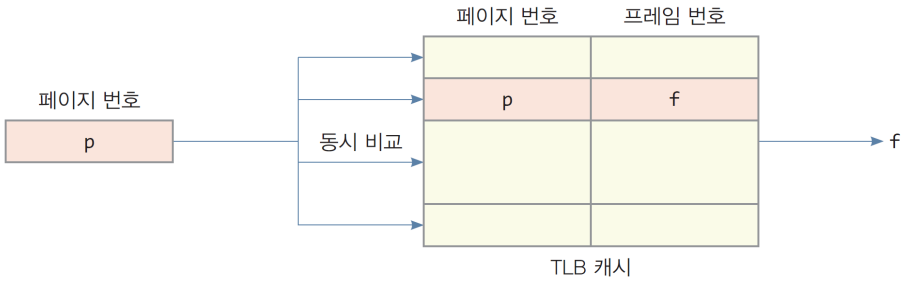
- MMU안에 위치하여, 최근에 접근한 ‘페이지와 프레임 번호’의 쌍을 항목으로 저장하는 캐시 메모리
- [페이지 번호 p, 프레임 번호 f]를 항목으로 저장 → 연관매핑
  - 페이지 번호를 받아 전체 캐시를 동시에 고속 검색 후 프레임 번호 출력
- Content-Addressable Memory(CAM) 또는 associative memory라고 불림
  - Content-Addressable인 이유: 데이터를 가지고 인덱스를 검색하기 때문
  - 비쌈…진짜 비쌈… 만들어보면 진짜 비쌈… → 크기 작음(64~1024 개의 항목 정도 저장)

TLB 메모리 엑세스

CPU로부터 논리 주소 발생
논리 주소의 페이지 번호가 TLB로 전달
페이지 번호와 TLB내 모든 항목 동시에 비교
- TLB에 페이지가 있는 경우, TLB hit
  - TLB에서 출력되는 프레임 번호와 offset 값으로 물리 주소 완성
- TLB에 페이지가 없는 경우, TLB miss → TLB는 miss 신호 발생
  - MMU는 페이지 테이블로부터 프레임 번호를 읽어와서 물리 주소 완성
  - 미스한 페이지의 [페이지번호, 프레임번호] 항목을 TLB에 삽입

아까 그 예제

가정
- 32비트 CPU, 페이지는 4KB
- 배열 n[100]의 논리 주소는 0x2000(페이지 2)부터 시작
- 배열 n[100]의 물리 주소는 0x7000(프레임 7)부터 시작
- 배열 n[100]의 크기는 400바이트이며 페이지2에 모두 들어 있음
- 페이지 테이블 2번의 주소: 0xA008
- 페이지 테이블은 물리 메모리 0xA000번지부터 시작

코드

  
int n[100]; // 400바이트
int sum = 0;
for(int i=0; i<100; i++)
    sum += n[i];

[i][j]로 접근하는 것?
- 0번 페이지, 1번 페이지, 2번 페이지 순서로 접근하기 때문에 처음 시도엔 미스나지만 두번째부터 캐시 히트가 나므로 속도 상승
[j][i]로 접근하는 것?
- 접근할 때마다 페이지를 다르게 접근해야 하므로 항상 캐시 미스 -> 메모리 접근 2번해야 함
- 느림
항상 캐시 히트가 나도록 하는 방법
- TLB 크기를 4라고 가정, Virtual Address에서 TLB에 접근할 때 항상 히트나려면?
- 프레임을 TLB 크기만큼으로만 나누자.
  - 단점: 내부 단편화 발생 가능(메모리 효율 저하)

TLB 성능

TLB와 참조의 지역성
- TLB는 참조의 지역성으로 인해 효과적인 전략임 → 순차 메모리 액세스 시에 실행 속도 빠름
- TLB 히트가 계속됨 (메모리의 페이지 테이블 액세스할 필요 없음)
- TLB를 사용하면, 랜덤 메모리 액세스나 반복이 없는 경우 실행 속도 느림
  - TLB 미스 자주 발생
  - TLB의 항목 교체(TLB 항목의 개수 제한되기 때문)
TLB 성능
- TLB 히트율 높이기 → TLB 항목 늘이기(비용과의 trade-off)
- 페이지 크기
  - 페이지가 클수록 TLB 히트 증가 → 실행 성능 향상
  - 페이지가 클수록 내부 단편화 증가 → 메모리 낭비
  - 이 둘 사이에는 trade-off 존재, 선택의 문제
  - 페이지가 커지는 추세: 요세는 메모리가 충분하므로. 디스크 입출력의 성능 향상을 위해
TLB reach
- TLB 도달 범위: TLB가 채워졌을 때, 미스없이 작동하는 메모리 액세스 범위
- TLB 항목 수 * 페이지 크기

7.2.2. 페이지 테이블 메모리 낭비 문제

32비트 CPU 환경에서 프로세스당 페이지 테이블 크기
- 프로세스의 주소 공간: 4GB/4KB = 2^32/2^12 = 2^20 = 약 100만개의 페이지로 구성
- 프로세스당 페이지 테이블의 크기:
  - 한 항목이 4바이트이면 2^20개 x 4바이트 = 4MB
  - 하나는 작다면 작은 크기라 볼 수 있지만, 시스템에서 돌아가는 프로세스 갯수를 생각해보면…?!
또한, 10MB의 메모리를 사용하는 프로세스가 있다고 하면
- 실제 활용되는 페이지 테이블 항목 수: 10MB/4KB = 10x2^20/2^12 = 10x2^8 = 2560개
- 실제 활용되는 페이지 테이블 비율 : 10x2^8x/2^20 = 10/2^12 = 0.0024
  - 매우 낮음
두가지 해결법
- 역 페이지 테이블(inverted page table, IPT)
- 멀티 레벨 페이지 테이블(multi-level page table)

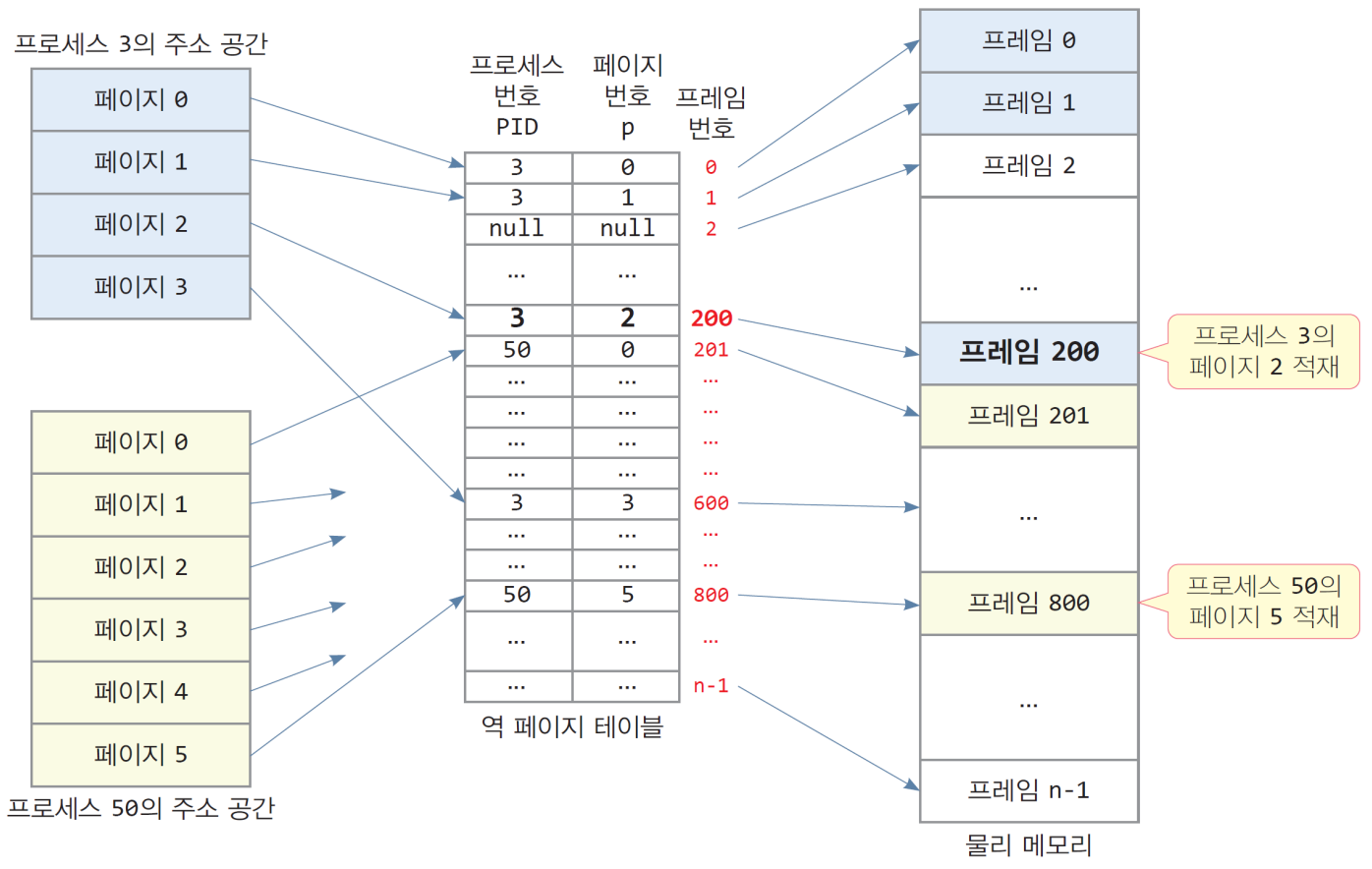
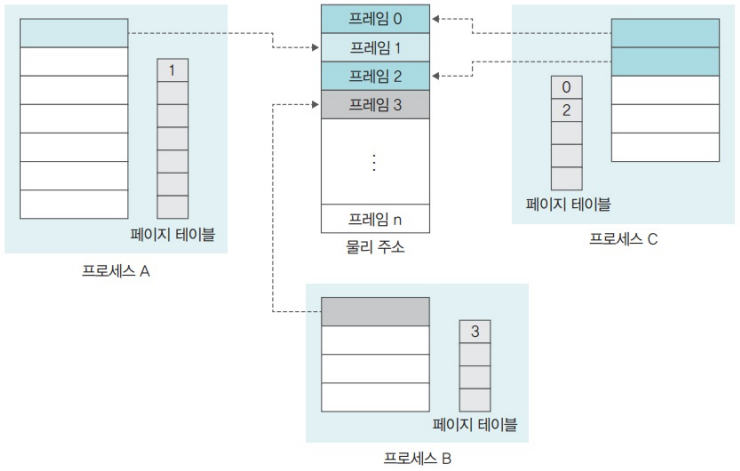
해결: 역 페이지 테이블(IPT)

물리 메모리의 프레임 번호를 기준으로 테이블을 작성한다.

시스템에 하나의 역 페이지 테이블만 둠
- 역 페이지 테이블 항목의 수 = 물리 메모리의 프레임 개수
역 페이지 테이블 항목
- [프로세스번호(pid), 페이지 번호(p)]
역 페이지 테이블의 인덱스
- 프레임 번호
역 페이지 테이블을 사용할 때 논리 주소 형식
- [프로세스번호, 페이지 번호, 옵셋]
역 페이지 테이블을 사용한 주소 변환
- VA=<PID, Page num., Offset>: 표기가 살짝 바뀐다!
- 논리 주소에서 (프로세스번호, 페이지 번호)로 역 페이지 테이블 검색
- 일치하는 항목을 발견하면 항목 번호가 바로 프레임 번호임
- 프레임 번호와 옵셋을 연결하면 물리 주소

상위 몇비트를 PID에 매핑이 되게 함
내부에서 페이지 번호를 매핑하고, 그 뒤에 offset을 매핑함

IPT를 이용한 주소공간의 접근

IPT의 크기

역 페이지 테이블의 개수
- 시스템에 1개 존재
역 페이지 테이블의 크기
- 역 페이지 테이블의 항목 크기: 프로세스 번호와 페이지 번호로 구성
- 프로세스 번호와 페이지 번호가 각각 4바이트라면, 항목 크기는 8 바이트
  - 상위는 20비트(page number) 하위는 12비트(offset)일 때
  - IPT는 32비트에 PID가 왼쪽에 더 붙어 관리가 됨 (PID)(32bit) -> 8바이트
  - PID를 4바이트로 퉁쳐놓아서 항목크기가 8바이트로 계산된 것임
- 역 페이지 테이블의 항목 수 = 물리 메모리 크기/프레임 크기
예) 물리 메모리가 4GB, 프레임 크기 4KB이면
- 테이블이 기존보다 가로로 더 커진 꼴임
- 역 페이지 테이블 항목 수 = 4GB/4KB = 2^20개 = 약 100만개(동일)
- 한 항목당 크기가 8바이트라면, 2^20개 항목 x 8바이트 = 8MB
- 기존 페이지 테이블과 비교해보면 (10개의 프로세스 기준)
  - 기존 페이지 테이블: 4MB x 10 = 40MB
    - 프로세스 수에 비례함
  - IPT: 8MB (1/5수준)
    - 프로세스 수와 상관 없이 딱 1개만 존재한다.

해결: 멀티레벨 페이지 테이블

현대에 주로 사용되는 방법
페이지 테이블을 수십~수백 개의 작은 페이지 테이블로 나누고 여러 레벨(level)로 구성
- 현재 사용 중인 페이지들에서 대해서만 페이지 테이블을 만드는 방식
- 기존 테이블의 낭비를 줄임
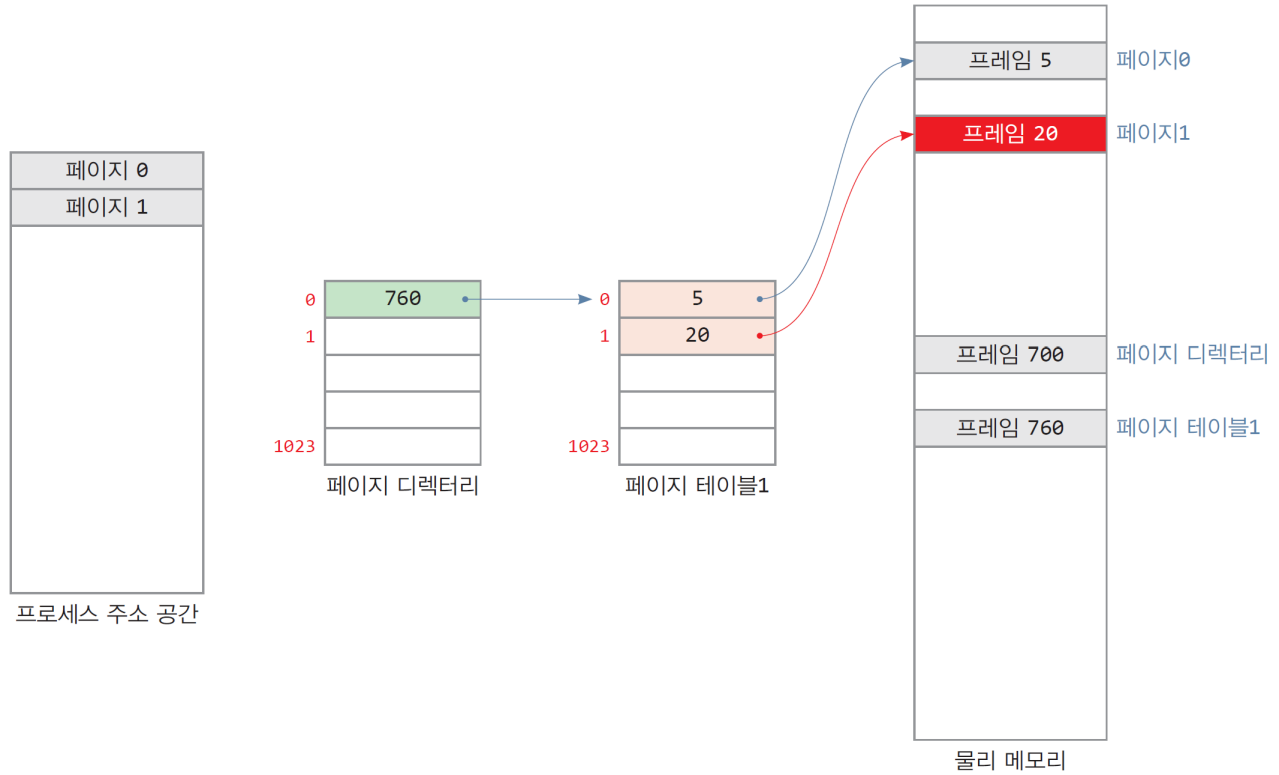
2-레벨로 멀티레벨 페이지 테이블를 구성하는 경우 (two-level paging scheme)
- VA = <Page directory index, Page num., offset> ~ 페이지 테이블들의 페이지화
  - 논리 주소의 하위 12비트 : 페이지 내 옵셋 주소
  - 논리 주소의 상위 20비트 : 페이지 디렉터리 인덱스와 페이지 테이블 인덱스
  - 페이지 디렉터리와 페이지 테이블의 트리 구조
  - 사용 중인 페이지들에 대해서만 페이지 테이블 할당

단점: 디렉토리만큼의 용량을 추가적으로 차지하게 됨

2-level page table

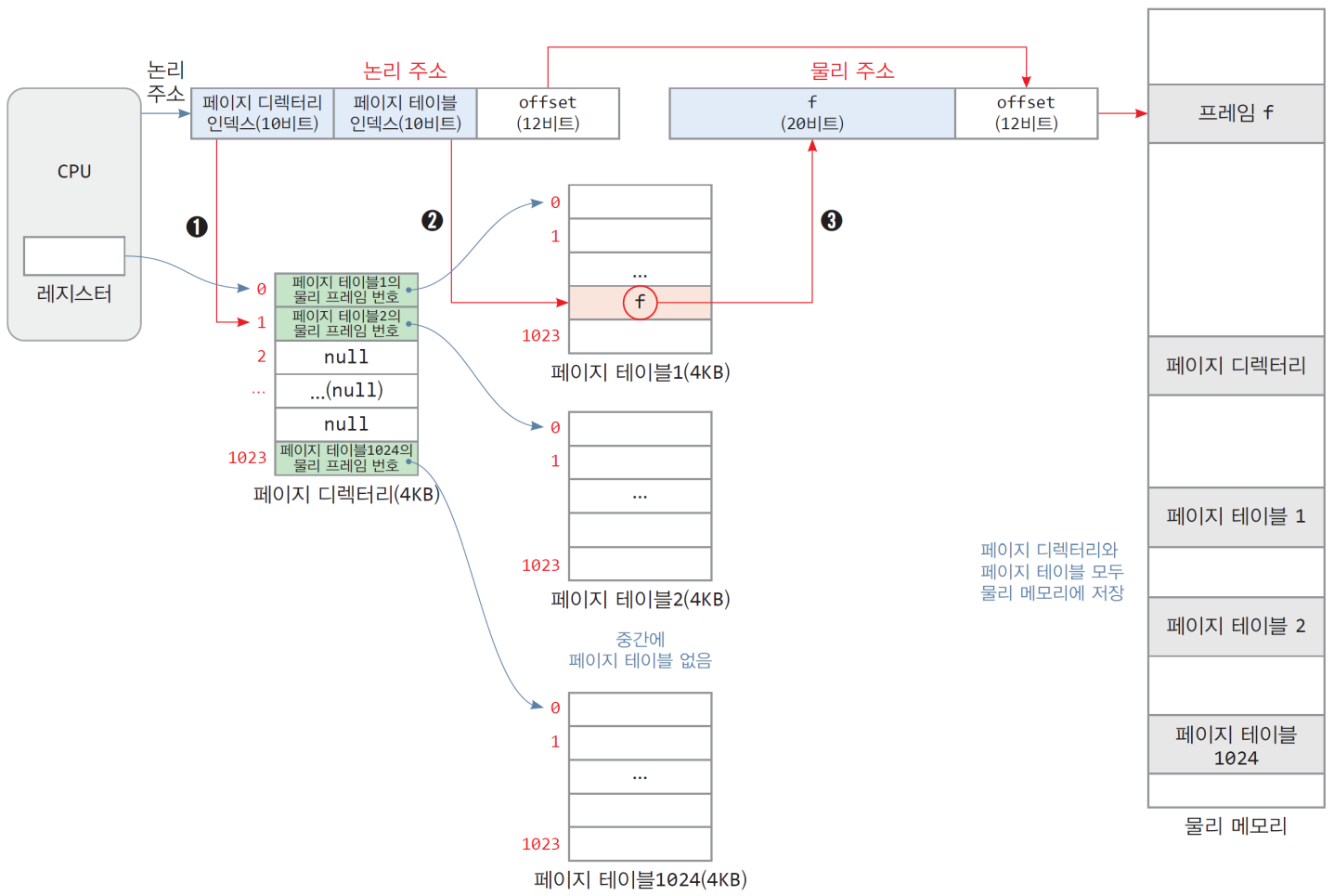
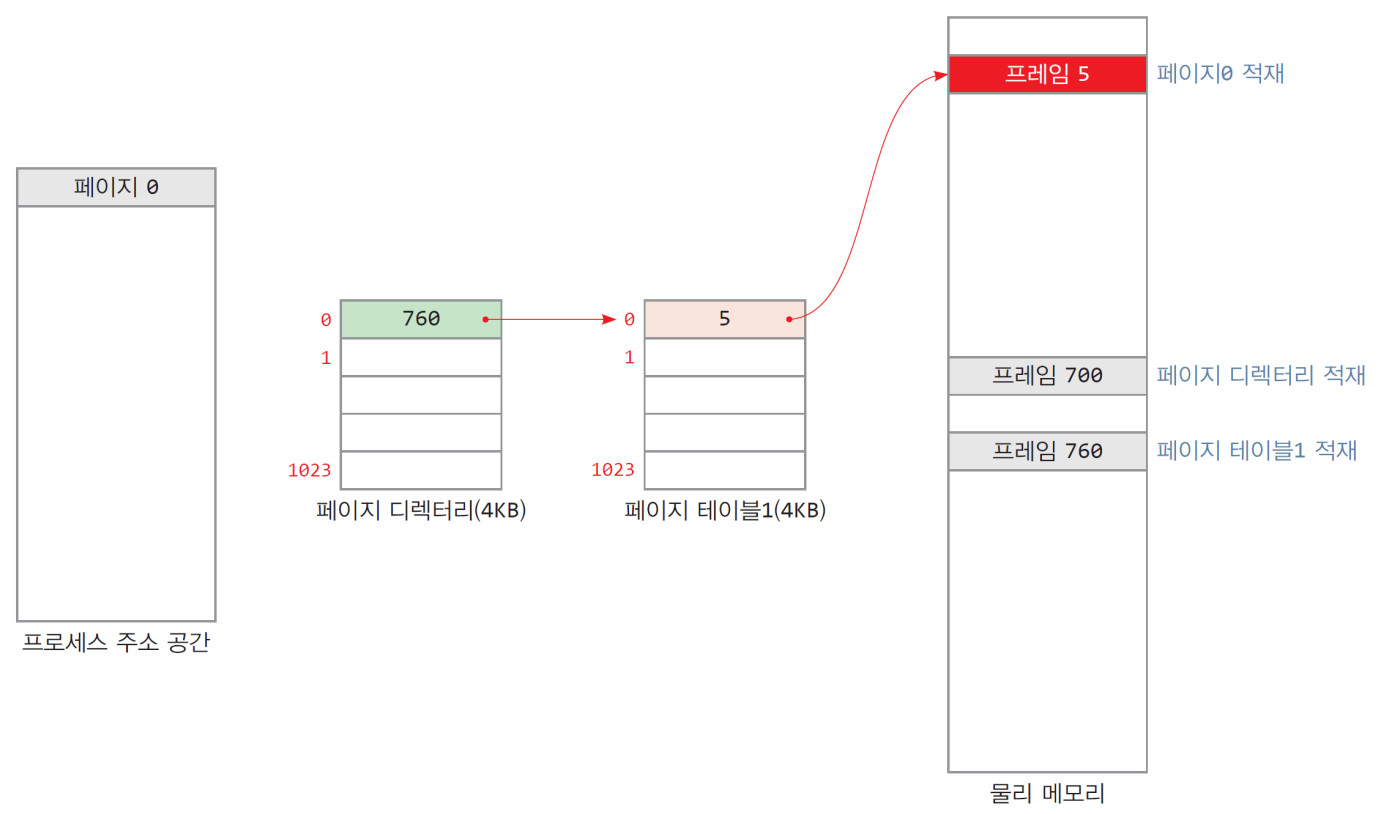
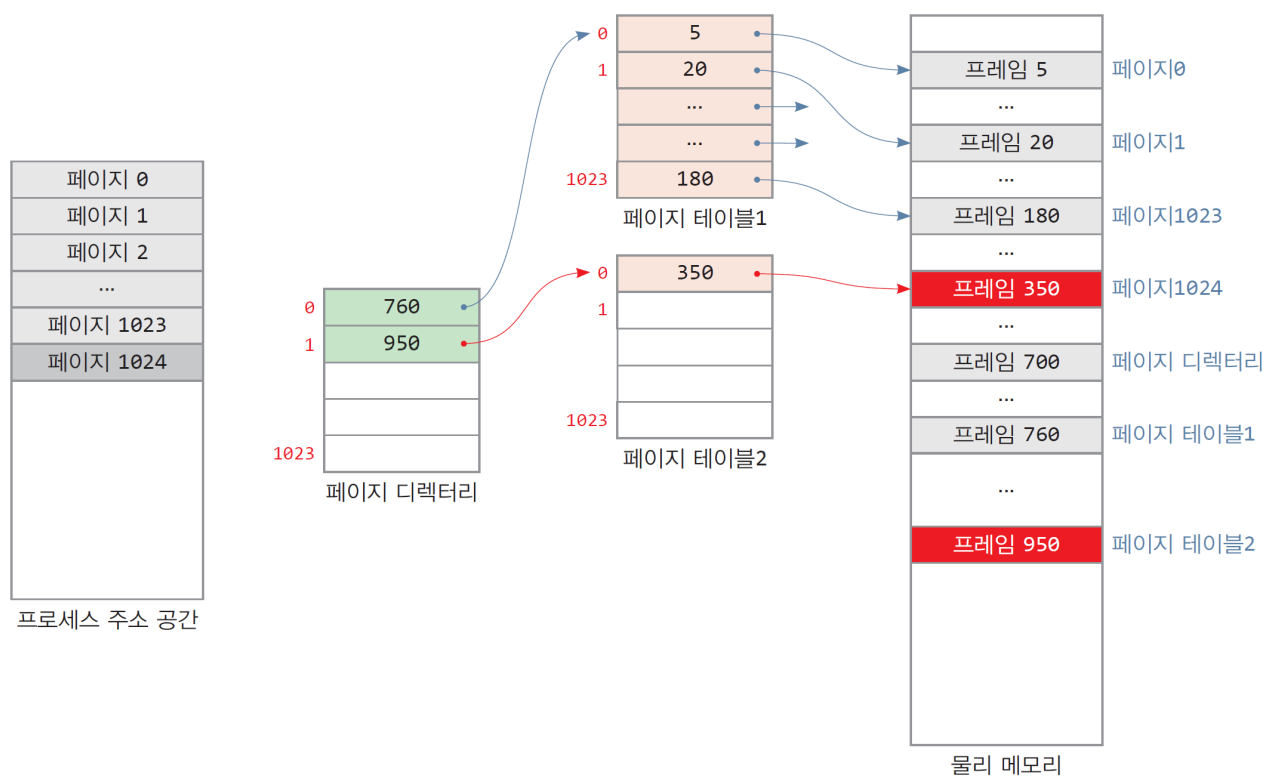
만들어지는 과정

시스템에는 페이지 디렉토리 테이블이 적재됨
- 프로세스의 0번 페이지가 적재되면 페이지 테이블 1 적재, 디렉토리와 연결됨

프로세스에 페이지 1이 추가되면 테이블1에 항목 추가

프로세스가 페이지 1024가 적제될 때(예: 테이블 크기 초과)
- 페이지 테이블 2 추가 생성 -> 디렉토리에 항목 추가됨

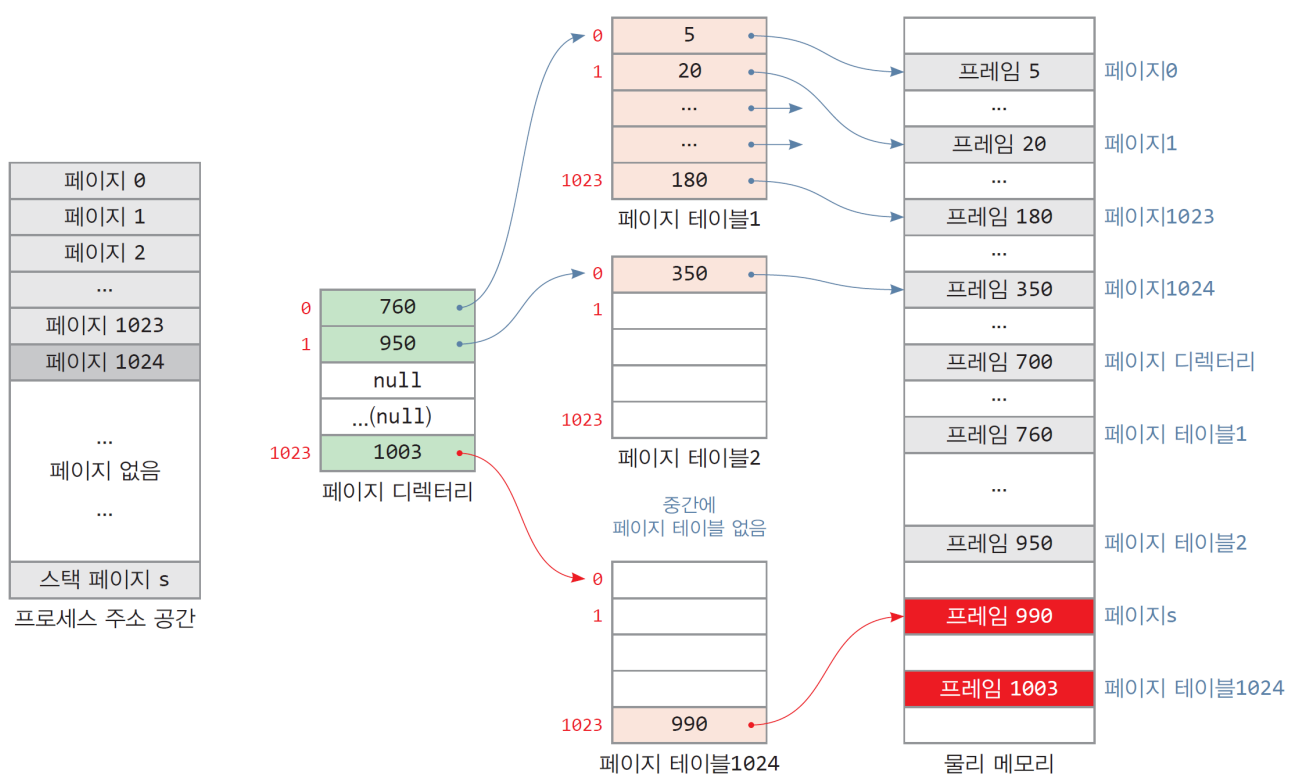
스택영역에 한 페이지가 추가되면 -> 페이지 테이블 추가 생성 -> 디렉토리 추가
이상의 예제에서,
- 테이블 총 크기: 디렉토리(4KB) + 3개의 테이블(12KB) = 16KB

2-level page table의 크기

2-레벨 페이지 테이블의 최대 메모리 소모량
- 페이지 디렉터리 1개 + 최대 1024개의 페이지 테이블
  - = 4KB + 1024*4KB = 4KB + 4MB
- 하지만, 일반적으로 프로세스는 1024개의 페이지 테이블을 모두 사용하지 않음
사례 1 – 프로세스가 1000개의 페이지로 구성
- 1000개의 페이지는 1개의 페이지 테이블에 의해 매핑 가능
- 메모리 소모량
  - 1개의 페이지 디렉터리와 1개와 1개의 페이지 테이블
    - = 4KB + 4KB = 8KB
사례 2 – 프로세스가 400MB 크기인 경우
- 프로세스의 페이지 개수 = 400MB/4KB = 100×1024 개
  - 100개의 페이지 테이블 필요
  - 메모리 소모량
  - 1개의 페이지 디렉터리와 100개의 페이지 테이블
  - = 4KB + 100×4KB = 404KB
기존 페이지 테이블의 경우 프로세스 크기에 관계없이 프로세스 당 4MB가 소모
2-레벨 페이지 테이블의 경우 페이지 테이블로 인한 메모리 소모를 확연히 줄일 수 있다.
단점: 속도 측면에선 느려진다.

현대에선 4-level page table을 사용한다고 한다.

7.3. 해시 페이지 테이블

여기까지 배운 내용들은 64비트 환경에서 사용하기는 어려워요!
- 64비트 주소 공간의 크기 = 16 엑사바이트… → 테이블 항목의 수가…?
- 페이지 크기가 8KB 라면, 2^64 / 2^16 = 281,474,976,710,656….
- 테이블 자체의 크기가 어마어마함. 검색도 어마어마하게 오래 걸림.
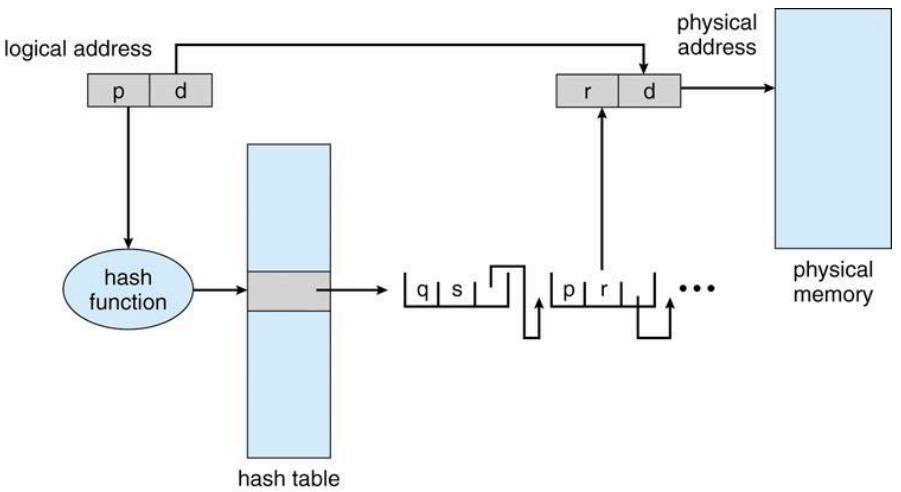
주소 공간이 32bit보다 크면 해시 값이 페이지 번호가 되는 해시형 페이지 테이블을 많이 사용.
- Page 테이블의 인덱스 p를 hash function의 입력값으로 넣어 나온 결과값으로 hash table을 검사하여 해당하는 Physical Memory를 검색
  - 같은 hash 결괏값에 대해서는 리스트를 이용하여 하나의 hash table 위치에 연결
전체 메모리를 안쓰므로 C나 파이썬에서 주소 찍어보면 항상 0x7FF로 시작함을 알 수 있음

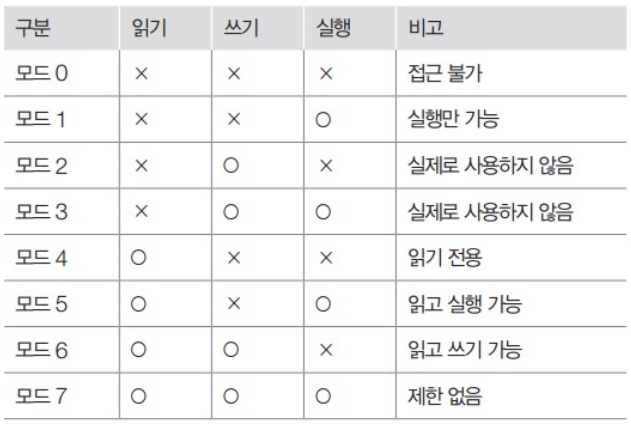
8. 메모리 접근 권한

메모리의 특정 번지에 저장된 데이터를 사용할 수 있는 권한
읽기(read), 쓰기(write), 실행(execute) 권한이 있음

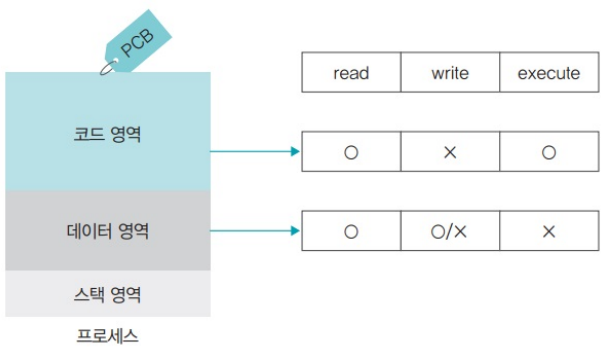
8.1. 프로세스의 영역별 메모리 접근 권한

코드 영역
- 자기 자신을 수정하는 프로그램은 없기 때문에 읽기 및 실행 권한을 가짐
데이터 영역
- 데이터는 크게 읽거나 쓸 수 있는 데이터와 읽기만 가능한 데이터로 나눌 수 있음
- (일반적인 변수는 읽거나 쓸 수 있으므로 읽기 및 쓰기 권한을 가지고 상수로 선언한 변수는 읽기 권한만 가짐)

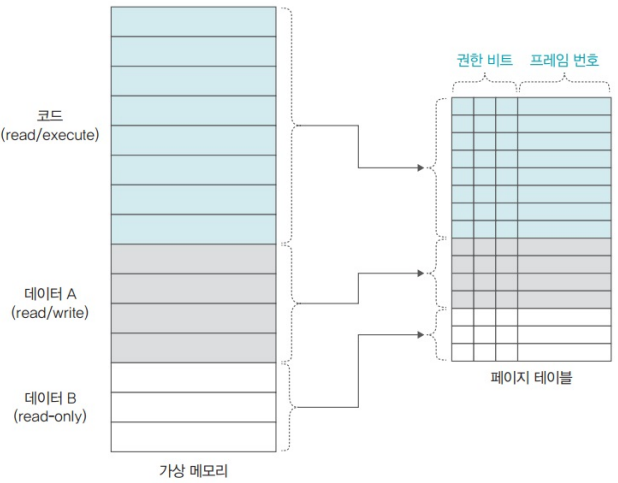
8.2. 메모리 접근 권한까지 고려한 페이지 테이블

페이지마다 접근 권한이 다르기 때문에 페이지 테이블의 모든 행에는 메모리 접근 권한과 관련된 권한 비트 추가
- 메모리 관리자는 주소 변환이 이루어질 때마다 페이지 테이블의 권한 비트를 이용하여 유용한 접근인지 아닌지 확인
단점:
- 페이지 테이블이 커진다! 어떻게 줄일 수 있을까?

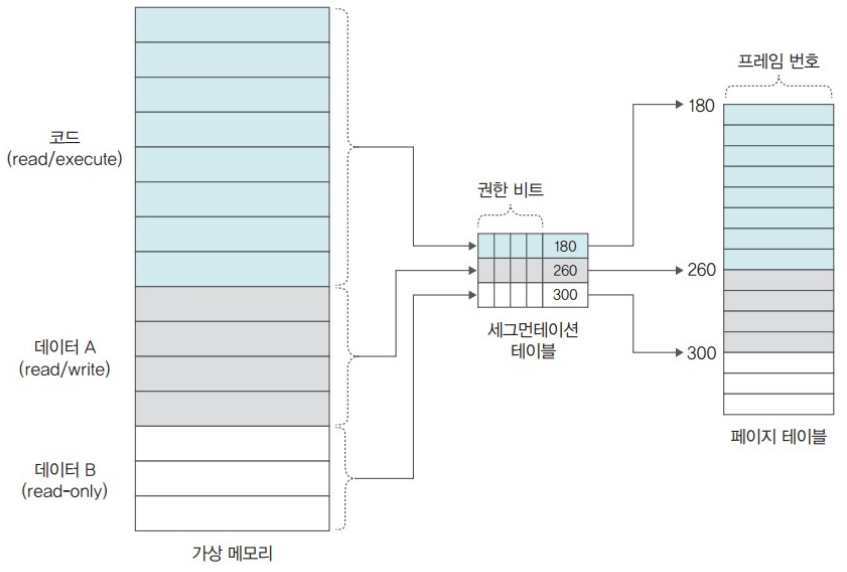
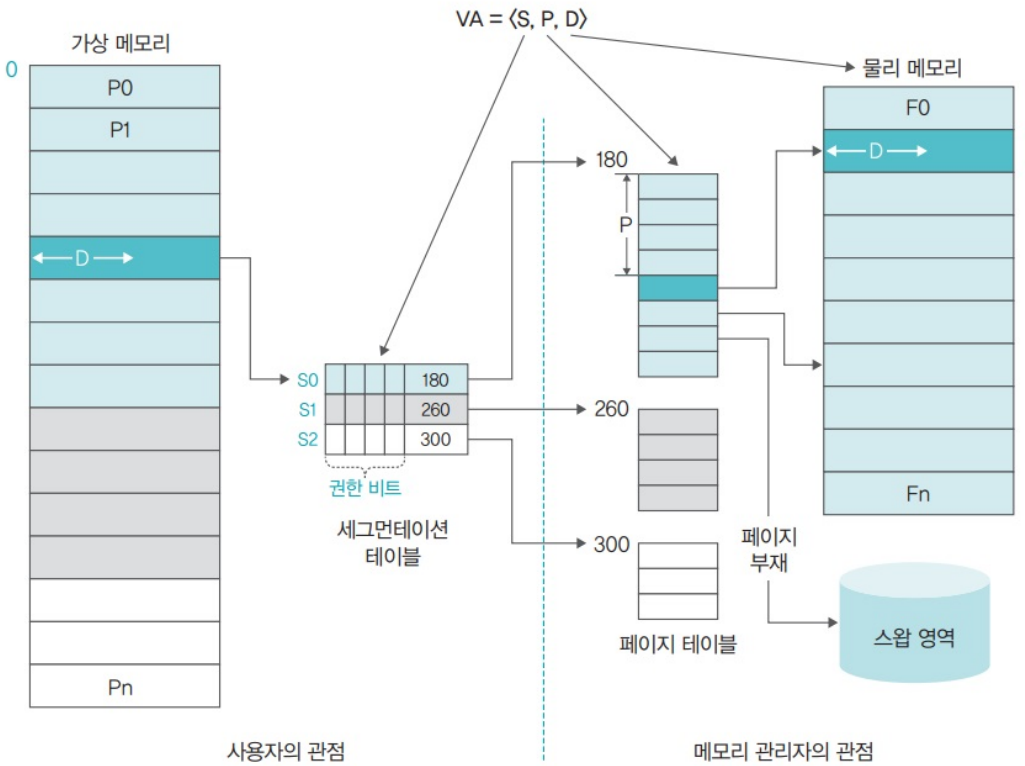
8.2.1. 해결: Segmentation-paging hybrid approach

세그먼테이션 테이블을 따로 둬서 구간마다 동일한 권한을 부여한다.
용량 절약

8.2.2. 세그먼테이션-페이징 혼용 기법에서 동적 주소 변환 과정

9. NX-bit(DEP in 윈도우)

쓰기 권한과 실행 권한을 절대로 동시에 주지 않겠다는 개념

9.1. NX-Bit ( Never eXecute Bit , 실행 방지 비트 )

프로세스 명령어나 코드 또는 데이터 저장을 위한 메모리 영역을 따로 분리하는 CPU의 기술
NX특성으로 지정된 모든 메모리 구역은 데이터 저장을 위해서만 사용되며, 프로세스 명령어가 그 곳에 상주하지 않음으로써 실행되지 않도록 만듦.
예: 메모리의 코드 영역은 실행 권한이 있다. 쓰기 권한이 있으면 해킹 위험이 있으므로 실행 권한과 쓰기 권한을 동시에 주지 않음

9.2. DEP ( Data Execution Prevention )

마이크로소프트 윈도우 운영 체제에 포함된 보안 기능
악의적인 코드가 실행되는 것을 방지하기 위해 메모리를 추가로 확인하는 하드웨어 및 소프트웨어 기술.
하드웨어 DEP: 메모리에 명시적으로 실행 코드가 포함되어 있는 경우를 제외하고 프로세스의 모든 메모리 위치에서 실행할 수 없도록 표시. 대부분의 최신 프로세스는 하드웨어 적용 DEP를 지원함
소프트웨어 DEP: CPU가 하드웨어 DEP를 지원하지 않을 경우 사용

9.3. Heap, Stack 영역에 Shellcode를 저장해서 실행하기 위해서는 해당 영역에 실행권한이 필요

DEP가 적용되지 않았을 경우에는 쉘코드가 실행이 됨
DEP가 적용된 경우에는 실행권한이 없으므로 쉘코드가 실행되지 않음.
프로그램에서 해당 동작에 대한 예외처리 후 프로세스가 종료 됩니다.

9.4. DEP 예시

추가 예정 이해할 필요 없고, 예제만 보여주는 것임

실행&쓰기 권한이 동시에 있는 것을 악용해 exploit code를 실행하게 하는 예제
따라할 필요 없음! 참고만 하자

Computer-Science, OS

OS 페이징

이 포스팅은 작성자의 CC BY-NC 4.0 라이선스를 준수합니다.