[DB] 관계대수와 연산자

1. 관계대수(relational algebra, 關係代數)

• 릴레이션에서 원하는 결과를 얻기 위해 수학의 대수와 같은 연산을 이용하여 질의하는 방법을 기술하는 언어

1.1. 관계대수와 관계해석

• 관계대수
  • 어떤 데이터를 어떻게 찾는지에 대한 처리 절차를 명시하는 절차적인 언어
  • DBMS 내부의 처리 언어로 사용됨
• 관계해석
  • 어떤 데이터를 찾는지만 명시하는 선언적인 언어
  • 관계대수와 함께 관계 DBMS의 표준 언어인 SQL의 이론적인 기반을 제공함

관계대수와 관계해석은 모두 관계 데이터 모델의 중요한 언어이며, 실제 동일한 표현 능력을 가지고 있다.

2. 관계의 수학적 의미

2.1. 릴레이션(relation)의 수학적 개념

$A = \lbrace 2, 4 \rbrace$, $B = \lbrace 1, 3, 5 \rbrace$라 하자. 그러면 카티전 프로덕트 $A \times B$ $=$ $\lbrace (2,1)$, $(2,3)$, $(2,5)$, $(4,1)$, $(4,3)$, $(4,5) \rbrace$ 이다.

• 릴레이션 $R$은 카티전 프로덕트($A \times B$)의 부분집합으로 정의함
  • 예시

\[\begin{aligned} R1 &= \lbrace (2, 1), (4, 1) \rbrace \\ R2 &= \lbrace (2, 1), (2, 3), (2, 5) \rbrace \\ R3 &= \lbrace (2, 3), (2, 5), (4, 3), (4, 5) \rbrace \end{aligned}\]

• 원소 개수가 $n$인 집합 $S$의 부분집합의 개수는 $2^{n}$임
  • 즉, (카티전 프로덕트 $A \times B$의 부분집합의 개수) $= 2^{|A| \times |B|}$
• 카티전 프로덕트의 기초 집합 $A$, $B$ 각각이 가질 수 있는 값의 범위를 도메인(domain)이라고 함
  • 즉, (집합 $A$의 도메인) $= \lbrace 2, 4 \rbrace$
• 릴레이션 역시 집합이므로 집합에서 집합에서 가능한 연산은 합집합($\cup$), 교집합($\cap$), 카티전 프로덕트($\times$) 등이 있음

\[\begin{aligned} R1 \cup R2 &= \lbrace(2, 1), (4, 1), (2, 3), (2, 5)\rbrace \\ R1 \cap R2 &= \lbrace(2, 1)\rbrace \end{aligned}\]

2.2. 릴레이션의 현실 세계 적용

학번 $= \lbrace 2, 4 \rbrace$, 과목 $= \lbrace$ 데이터베이스, 자료구조, 프로그래밍 $\rbrace$라고 하자.

• 두 집합의 카티전 프로덕트( 학번 $\times$ 과목)은 학번 원소와 과목 원소의 순서쌍의 집합임
  • 즉, (학번 $\times$ 과목) $= \lbrace (2,$ 데이터베이스$), (2,$ 자료구조$), (2,$ 프로그래밍$), (4,$ 데이터베이스$), (4,$ 자료구조$), (4,$ 프로그래밍$) \rbrace$ 을 말한다.
• (학번 $\times$ 과목)의 각 원소는 학생이 과목을 수강할 수 있는 모든 경우를 나열한 것이다.
• 수강 $= \lbrace (2,$ 데이터베이스$), (2,$ 자료구조$), (4,$ 프로그래밍$) \rbrace$은 카티전 프로덕트 (학번 $\times$ 과목)의 부분집합으로 하나의 릴레이션 인스턴스이다.

---

• 수강 릴레이션

학번	과목
2	데이터베이스
2	자료구조
4	프로그래밍

수강 릴레이션의 각 튜플은 카티전 프로덕트 (학번 $\times$ 과목)의 원소 중 하나로, 수강 테이블을 데이터베이스에서는 릴레이션(relation)이라고 한다.

3. 관계대수 연산자

3.1. 기본 연산자들

연산자 종류	대상	연산자 이름	기호	설명
기본	단항	셀렉션	$\sigma$	릴레이션에서 조건에 만족하는 튜플을 선택
기본	단항	프로젝션	$\pi$	릴레이션의 속성을 선택
추가	단항	개명	$\rho$	릴레이션이나 속성의 이름을 변경
유도	이항	디비전	$\div$	부모 릴레이션에 포함된 튜플의 값을 모두 갖고 있는 튜플을 분자 릴레이션에서 추출
기본	이항	합집합	$\cup$	두 릴레이션의 합집합
기본	이항	차집합	$−$	두 릴레이션의 차집합
유도	이항	교집합	$\cap$	두 릴레이션의 교집합
기본	이항	카디전 프로덕트	$\times$	두 릴레이션에 속한 모든 튜플의 집합

3.2. 조인 연산자들

조인 연산자들은 모두 다음의 특성을 갖는다.

• 연산자 종류: 유도
• 대상: 이항

연산자 이름	기호	설명
세타	${\large\bowtie}_{\small\theta}$	두 릴레이션 간의 비교 조건에 만족하는 집합
동등	${\large\bowtie}$	두 릴레이션 간의 같은 값을 가진 집합
자연	${\large\bowtie}_{\small N}$	동등 조인에서 중복 속성을 제거
세미 left	${\large\ltimes}$	자연 조인 후 오른쪽 속성을 제거
세미 right	${\large\rtimes}$	자연 조인 후 왼쪽 속성을 제거
외부 left	$⟕$	자연 조인 후 left 값을 결과로 추출
외부 right	$⟖$	자연 조인 후 right 값을 결과로 추출
외부 full	$⟗$	자연 조인 후 full 값을 결과로 추출

• 외부 조인(left, right, full) 추가 설명
  • 외부 조인이 실패할 경우(또는 값이 없을 경우), 한 쪽의 값을 NULL로 채운다.

4. 관계대수식

• 관계대수: 릴레이션 간 연산을 통해 결과 릴레이션을 찾는 절차를 기술한 언어
• 관계대수식(relational algebra expression): 관계대수 연산을 수행하기 위한 식
  • 릴레이션, 연산자로 구성됨
  • 결과는 릴레이션으로 반환됨
  • 반환된 릴레이션은 릴레이션의 모든 특징을 따른다.

• 단항 연산자: $\mathrm{op}_{<\mathrm{condition}>} \; \mathrm{Rel}$
• 이항 연산자: $\mathrm{Rel1 \; op}_{<\mathrm{condition}>} \; \mathrm{Rel2}$

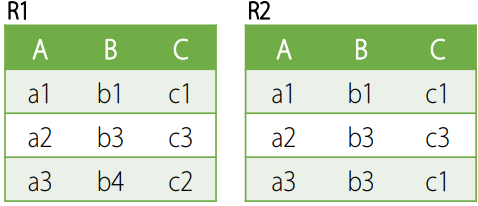
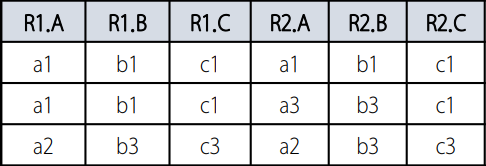
다음은 관계대수식을 이해하기 위한 예제 데이터(릴레이션)이다.

관계대수식을 이해하기 위한 예제 데이터

4.1. Selection($\sigma$)

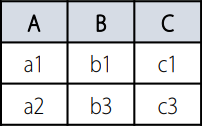
• $\sigma_{A=a1 \; \mathrm{or} \; A=a2}(R1)$
  • 조건에 맞는 튜플을 추출한다.

Selection 결과

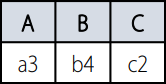
4.2. Projection($\pi$)

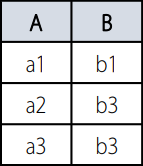
• $\pi_{A, B}(R2)$
  • R2에서 조건에 맞는 속성만을 추출한다.

Projection 결과

4.3. 합집합($\cup$)

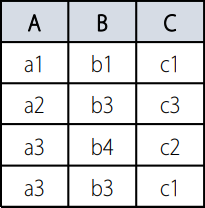
• $R1 \cup R2$
  • $R1$과 $R2$의 합집합을 구한다.

합집합 결과

4.4. 차집합($-$)

• $R1 - R2$
  • $R1$과 $R2$의 차집합을 구한다.

차집합 결과

4.5. Join

• $R1 \; {\large\bowtie}_{R1.C = R2.C} \; R2$
  • $R1$과 $R2$의 카티전 프로덕트를 구하여, 조건에 맞는 튜플을 추출한다.

Join 결과